题目内容
已知函数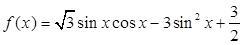 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)已知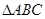 中,角
中,角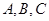 所对的边长分别为
所对的边长分别为 ,若
,若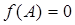 ,
,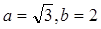 ,求
,求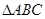 的面积
的面积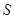 .
.
(1)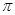 ;(2)
;(2)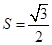 .
.
解析试题分析:(1)利用二倍角公式的变形: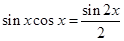 ,
,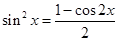 及辅助角公式,可将
及辅助角公式,可将 化简为
化简为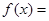
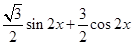
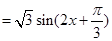 ,从而
,从而 的最小正周期为
的最小正周期为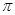 ;(2)由(1)及
;(2)由(1)及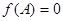 ,可得:
,可得: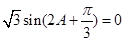 ,根据
,根据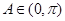 可得
可得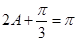 或
或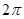 ,从而
,从而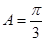 或
或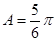 (
(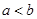 ,舍去),再利用正弦定理
,舍去),再利用正弦定理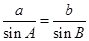 ,从而得
,从而得 ,则
,则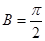 ,
,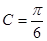 , 因此
, 因此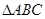 的面积
的面积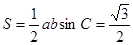 .
.
试题解析:(1)∵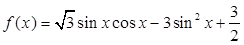 ,
,
∴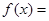
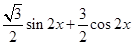
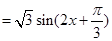 , ∴
, ∴ 的最小正周期为
的最小正周期为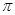 ;
;
(2)由(1)及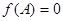 ,∴
,∴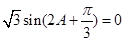 ,又∵
,又∵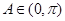 ,∴
,∴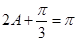 或
或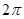 ,
,
∴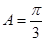 或
或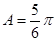 ,又∵
,又∵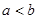 ,∴
,∴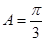 ,由正弦定理:
,由正弦定理: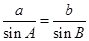 ,得
,得 ,则
,则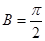 ,
,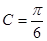 , ∴
, ∴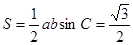 .
.
考点:1.三角恒等变形;2.正弦定理解三角形.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
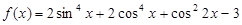 .
.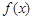 的最小正周期.
的最小正周期.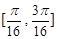 上的最小值并求当
上的最小值并求当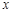 的取值集合.
的取值集合. ;
; 的周期和单调递增区间;
的周期和单调递增区间; 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围. (米)是时间
(米)是时间 (
( ,单位:小时,
,单位:小时, 表示0:00—零时)的函数,其函数关系式为
表示0:00—零时)的函数,其函数关系式为

 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
.已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米. 的表达式;
的表达式;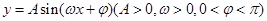 ,
,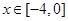 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,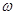 和
和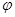 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设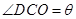 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)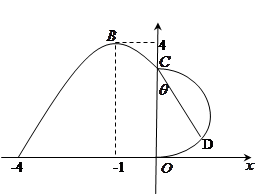
 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ) 的图象如图所示.
的图象如图所示.
 的解.
的解. .
.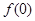 的值;
的值; ,求
,求 的值.
的值. .
. ,且
,且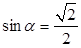 ,求
,求 的值;
的值; 的最小正周期及单调递增区间.
的最小正周期及单调递增区间. ,
, .
. ,求
,求 的最大值及相应的
的最大值及相应的 的取值集合;
的取值集合; 是
是 ,求
,求 的值和
的值和