题目内容
已知函数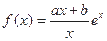 (
(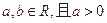 ).
).
(1)若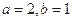 ,求函数
,求函数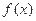 的极值;
的极值;
(2)设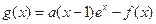 .
.
① 当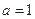 时,对任意
时,对任意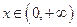 ,都有
,都有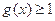 成立,求
成立,求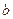 的最大值;
的最大值;
② 设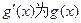 的导函数.若存在
的导函数.若存在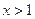 ,使
,使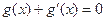 成立,求
成立,求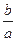 的取值范围.
的取值范围.
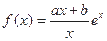 (
(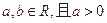 ).
).(1)若
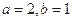 ,求函数
,求函数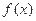 的极值;
的极值;(2)设
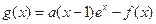 .
.① 当
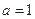 时,对任意
时,对任意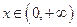 ,都有
,都有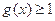 成立,求
成立,求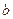 的最大值;
的最大值;② 设
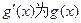 的导函数.若存在
的导函数.若存在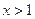 ,使
,使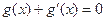 成立,求
成立,求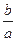 的取值范围.
的取值范围.(1)极大值是e-1,极小值
(2)①-1-e-1 ②(-1,+∞)

(2)①-1-e-1 ②(-1,+∞)
(1)当a=2,b=1时,f (x)=(2+ )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).
所以f ′(x)= ex
ex
令f ′(x)=0,得x1=-1,x2= ,列表
,列表
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f ( )=
)=
(2)① 因为g (x)=(ax-a)ex-f (x)=(ax- -2a)ex,
-2a)ex,
当a=1时,g (x)=(x- -2)ex.
-2)ex.
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以b≤x2-2x- 在x∈(0,+∞)上恒成立. 记h(x)=x2-2x-
在x∈(0,+∞)上恒成立. 记h(x)=x2-2x- (x>0),则h′(x)=
(x>0),则h′(x)= .
.
当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数;
所以h(x)min=h(1)=-1-e-1;所以b的最大值为-1-e-1. ②因为g (x)=(ax- -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=( +ax-
+ax- -a)ex.
-a)ex.
由g (x)+g′(x)=0,得(ax- -2a)ex+(
-2a)ex+( +ax-
+ax- -a)ex=0,
-a)ex=0,
整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g (x)+g ′(x)=0成立.
等价于存在x>1,2ax3-3ax2-2bx+b=0成立.
因为a>0,所以 =
= .
.
设u(x)= (x>1),则u′(x)=
(x>1),则u′(x)= .
.
因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以 >-1,即
>-1,即 的取值范围为(-1,+∞)
的取值范围为(-1,+∞)
 )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).所以f ′(x)=
 ex
ex令f ′(x)=0,得x1=-1,x2=
 ,列表
,列表| x | (-∞,-1) | -1 | (-1,0) | (0,  ) ) |  | ( ,+∞) ,+∞) |
| f ′(x) |  |  | - | - |  |  |
| f (x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f (
 )=
)=
(2)① 因为g (x)=(ax-a)ex-f (x)=(ax-
 -2a)ex,
-2a)ex,当a=1时,g (x)=(x-
 -2)ex.
-2)ex.因为g (x)≥1在x∈(0,+∞)上恒成立,
所以b≤x2-2x-
 在x∈(0,+∞)上恒成立. 记h(x)=x2-2x-
在x∈(0,+∞)上恒成立. 记h(x)=x2-2x- (x>0),则h′(x)=
(x>0),则h′(x)= .
.当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数;
所以h(x)min=h(1)=-1-e-1;所以b的最大值为-1-e-1. ②因为g (x)=(ax-
 -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=( +ax-
+ax- -a)ex.
-a)ex.由g (x)+g′(x)=0,得(ax-
 -2a)ex+(
-2a)ex+( +ax-
+ax- -a)ex=0,
-a)ex=0,整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g (x)+g ′(x)=0成立.
等价于存在x>1,2ax3-3ax2-2bx+b=0成立.
因为a>0,所以
 =
= .
.设u(x)=
 (x>1),则u′(x)=
(x>1),则u′(x)= .
.因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以
 >-1,即
>-1,即 的取值范围为(-1,+∞)
的取值范围为(-1,+∞)
练习册系列答案
相关题目
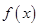 满足如下条件:当
满足如下条件:当 时,
时,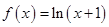 ,且对任
,且对任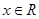 ,都有
,都有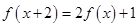 .
.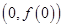 处的切线方程;
处的切线方程;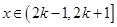 ,
,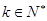 时,函数
时,函数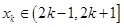 ,
,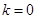 、
、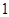 、
、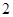 、
、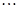 、
、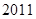 ,使得等式
,使得等式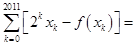
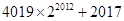 成立?若存在就求出
成立?若存在就求出 (
(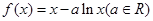
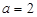 时,求曲线
时,求曲线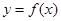 在点
在点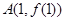 处的切线方程;
处的切线方程;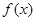 的极值.
的极值.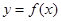 的导函数
的导函数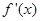 的图像如图所示,则
的图像如图所示,则
 ,
,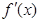 为
为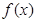 的导函数。 (1)求函数
的导函数。 (1)求函数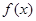 的单调递减区间;
的单调递减区间;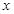 ,有
,有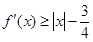 成立,求
成立,求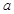 的取值范围;
的取值范围; 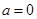 时,在曲线
时,在曲线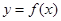 上是否存在两点
上是否存在两点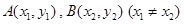 ,使得曲线在
,使得曲线在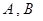 两点处的切线均与直线
两点处的切线均与直线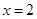 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由. 上过点(1,0)的切线方程( )
上过点(1,0)的切线方程( )



 与
与 的图象在
的图象在 处有相同的切线,
处有相同的切线, = .
= .