题目内容
3.在锐角三角形ABC中,a,b,c分别为内角A,B,C的对边,若A=2B,a=6,b=4,则c=5.分析 由A=2B,a=6,b=4,则sinA=sin2B=2sinBcosB,运用正弦定理和余弦定理,计算解方程可得c=4或5,再由最大边所对角最大,运用余弦定理,即可判断.
解答 解:由A=2B,a=6,b=4,
则sinA=sin2B=2sinBcosB,
由正弦定理和余弦定理可得,
a=2b•a2+c2−b22aca2+c2−b22ac,
即有36c=4(36+c2-16),
解得c=4或5,
当c=4时,a最大,由余弦定理可得cosA=b2+c2−a22bcb2+c2−a22bc
=16+16−362×4×416+16−362×4×4<0,即A为钝角,不合题意,舍去;
当c=5时,a最大,由余弦定理可得cosA=b2+c2−a22bcb2+c2−a22bc
=16+25−362×4×516+25−362×4×5>0,即A为锐角,合题意.
故答案为:5.
点评 本题考查正弦定理和余弦定理的运用,同时考查三角函数的化简,考查运算能力,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
11.设直线x+y=1与抛物线y2=2px(p>0)交于A,B两点,若OA⊥OB,则△OAB的面积为( )
| A. | 1 | B. | 12√5 | C. | √5 | D. | 2 |
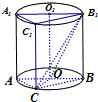 如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P
如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P