题目内容
5.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=sin(2x-$\frac{π}{6}$).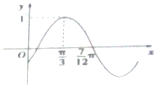
分析 由图象可得T=4($\frac{7π}{12}-\frac{π}{3}$)=$π=\frac{2π}{ω}$,从而解得ω,由于点($\frac{7π}{12}$,0)在函数图象上,结合范围|φ|<$\frac{π}{2}$,从而解得φ,即可求得函数解析式.
解答 解:由图象可得:T=4($\frac{7π}{12}-\frac{π}{3}$)=$π=\frac{2π}{ω}$,从而解得:ω=2,
由于点($\frac{7π}{12}$,0)在函数图象上,可得:sin(2×$\frac{7π}{12}$+φ)=0,解得φ=kπ-$\frac{7π}{6}$,k∈Z.
由于|φ|<$\frac{π}{2}$,从而解得φ=-$\frac{π}{6}$,
即有:f(x)=sin(2x-$\frac{π}{6}$).
故答案为:sin(2x-$\frac{π}{6}$).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.正方形ABCD中,M为AD中点,在线段AB上任取一点P,在线段DC上任取一点Q,则么∠PMQ为锐角的概率为( )
| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{3π}{16}$ | D. | $\frac{16-3π}{16}$ |
20.已知数列{an}是等比数列,a1,a2,a3依次位于表中第一行,第二行,第三行中的某一格内,又a1,a2,a3中任何两个都不在同一列,则an=2•3n-1(n∈N*).
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 1 | 10 | 2 |
| 第二行 | 6 | 14 | 4 |
| 第三行 | 9 | 18 | 8 |
14.如图直观图由直三棱柱与圆锥组成的几何体,其三视图的正视图为正方形,则俯视图中的椭圆的离心率为( )


| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
 甲、乙两同学5次综合评测的成绩如茎叶图所示.老师发现乙同学成绩的一个数字无法看清.但老师知道乙的平均成绩超过甲的平均成绩,则看不清楚的数字为9.
甲、乙两同学5次综合评测的成绩如茎叶图所示.老师发现乙同学成绩的一个数字无法看清.但老师知道乙的平均成绩超过甲的平均成绩,则看不清楚的数字为9.