题目内容
16.正方形ABCD中,M为AD中点,在线段AB上任取一点P,在线段DC上任取一点Q,则么∠PMQ为锐角的概率为( )| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{3π}{16}$ | D. | $\frac{16-3π}{16}$ |
分析 利用两角和的正切公式,利用线性规划,以及几何概型的概率公式即可得到结论
解答 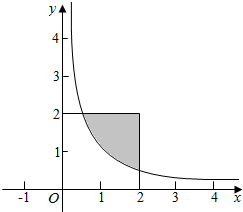 解:设正方形的边长为2,AP=x,DQ=y,
解:设正方形的边长为2,AP=x,DQ=y,
则0≤x≤,2,0≤y≤2,平面区域{(x,y)|0≤x≤2,0≤y≤2}对应的区域面积S=4.
则tan∠QMD=$\frac{DQ}{DM}$=y,tan∠AMP=$\frac{AP}{AM}$=x,
则tan(∠QMD+∠AMP)=$\frac{tan∠QMD+tan∠AMP}{1-tan∠QMDtan∠AMP}$=$\frac{x+y}{1-xy}$,
若∠PMQ为锐角,则等价为∠QMD+∠AMP是钝角,
即tan(∠QMD+∠AMP)=$\frac{x+y}{1-xy}$<0,
即1-xy<0,即y>$\frac{1}{x}$,
作出对应的平面区域如图:
当y=2时,由y=$\frac{1}{x}$,解得x=$\frac{1}{2}$,满足y>$\frac{1}{x}$的部分如图阴影部分,其面积为:${∫}_{\frac{1}{2}}^{2}(2-\frac{1}{x})dx$=(2x-lnx)|${\;}_{\frac{1}{2}}^{2}$=3-2ln2,
由几何概型公式得到∠PMQ为锐角的概率为$\frac{3-ln2}{4}$;
故选:A.
点评 本题主要考查几何概型的概率计算,根据条件将∠PMQ为锐角进行转化,利用积分求出对应区域的面积是解决本题的关键,综合性较强,涉及的知识点较多.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
7.直线y=2x与曲线y=x3围成的封闭图形的面积是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
11.“m=1”是“函数f(x)=(m2-4m+4)x2”为幂函数的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |