题目内容
在数列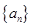 中,
中,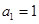 ,
,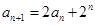 .
.
(1)设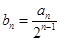 .证明:数列
.证明:数列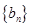 是等差数列;
是等差数列;
(2)求数列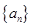 的前
的前 项和
项和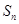 .
.
(1)详见解析;(2)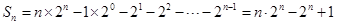 .
.
解析试题分析:(1)题中条件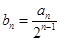 ,而要证明的是数列
,而要证明的是数列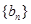 是等差数列,因此需将条件中所给的
是等差数列,因此需将条件中所给的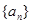 的递推公式
的递推公式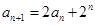 转化为
转化为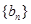 的递推公式:
的递推公式: ,从而
,从而 ,
, ,进而得证;(2)由(1)可得,
,进而得证;(2)由(1)可得, ,因此数列
,因此数列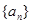 的通项公式可以看成一个等差数列与等比数列的乘积,故可考虑采用错位相减法求其前
的通项公式可以看成一个等差数列与等比数列的乘积,故可考虑采用错位相减法求其前 项和,即有:
项和,即有: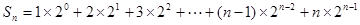 ①,①
①,① 得:
得: ②,
②,
②-①得 .
.
试题解析:(1)∵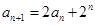 ,
,  ,又∵
,又∵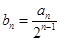 ,∴
,∴ ,
, ,∴则
,∴则 是
是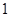 为首项
为首项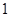 为公差的等差数列;
为公差的等差数列;
由(1)得  ,∴
,∴ ,
,
∴ ①,
①,
① 得:
得: ②,
②,
②-①得 .
.
考点:1.数列的通项公式;2.错位相减法求数列的和.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
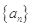 中,
中, 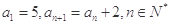 ,那么此数列的前10项和
,那么此数列的前10项和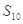 = .
= . 的前n项和为
的前n项和为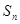 ,公差
,公差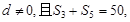
 成等比数列
成等比数列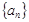 的通项公式;
的通项公式;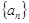 中依次取出第2项、第4项、第8项,
中依次取出第2项、第4项、第8项,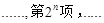 ,按原来顺序组成一个新数列
,按原来顺序组成一个新数列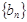 ,且这个数列的前
,且这个数列的前 的表达式.
的表达式. 的前
的前 项和
项和 ,数列
,数列 满足
满足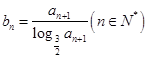 .
.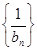 的前
的前 .
. 的前n项和为
的前n项和为 ,且满足
,且满足 ,
,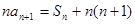 .
.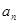 ;
; 为数列{
为数列{ }的前n项和,求
}的前n项和,求 ,证明:
,证明: .
.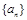 的前n项和为
的前n项和为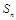 ,且
,且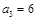 ,
,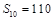 .
.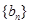 前n项和为
前n项和为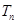 ,且
,且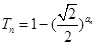 ,令
,令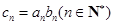 .求数列
.求数列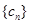 的前n项和
的前n项和 .
. 中,
中, ,且对于任意正整数n,都有
,且对于任意正整数n,都有 ,则
,则 =______
=______ 中,
中,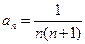 ,前n项和为Sn,则S2009=______________。
,前n项和为Sn,则S2009=______________。