题目内容
设直线过点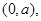 其斜率为1,且与圆
其斜率为1,且与圆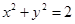 相切,则
相切,则 的值为
的值为
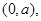 其斜率为1,且与圆
其斜率为1,且与圆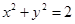 相切,则
相切,则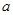 的值为
的值为 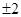
本试题主要是考查了直线与圆相切的位置关系的运用。
设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,设直线方程为y=x+a,根据直线与圆相切可知,圆心(0,0)到直线的距离等于半径 ,
,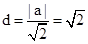 ,∴a的值为±2,故填写为
,∴a的值为±2,故填写为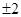 。
。
解决该试题的关键是直线与圆相切时,圆心到直线的距离等于圆的半径得到结论。
设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,设直线方程为y=x+a,根据直线与圆相切可知,圆心(0,0)到直线的距离等于半径
 ,
,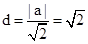 ,∴a的值为±2,故填写为
,∴a的值为±2,故填写为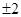 。
。解决该试题的关键是直线与圆相切时,圆心到直线的距离等于圆的半径得到结论。

练习册系列答案
相关题目
 发出的光线
发出的光线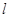 射到
射到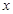 轴上,被
轴上,被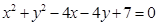 相切,求光线
相切,求光线 的端点
的端点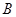 的坐标为
的坐标为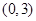 ,端点
,端点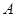 在
在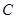 :
: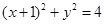 上运动。
上运动。 的轨迹方程;
的轨迹方程; 与圆
与圆 ,弦
,弦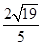 ,求直线
,求直线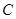 与直线
与直线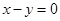 及
及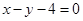 都相切,圆心在直线
都相切,圆心在直线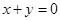 上,则圆
上,则圆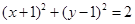
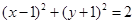
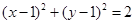
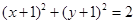
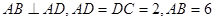 ,动点P在以点C为圆心且与直线BD相切的圆上运动,设
,动点P在以点C为圆心且与直线BD相切的圆上运动,设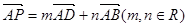 ,则
,则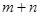 的取值范围是 。
的取值范围是 。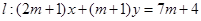 ,圆
,圆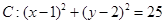
 和圆
和圆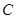 的位置关系;
的位置关系;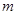 的值.
的值.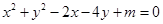 .
.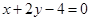 相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
相交于M、N两点,且OM⊥ON(O为坐标原点),求m;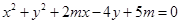 表示一个圆,
表示一个圆,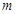 的取值范围;
的取值范围;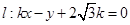 相交,求直线
相交,求直线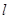 的倾斜角的取值范围.
的倾斜角的取值范围.