题目内容
已知直线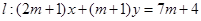 ,圆
,圆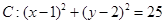
(1)判断直线 和圆
和圆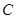 的位置关系;
的位置关系;
(2)若直线 和圆
和圆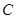 相交,求相交弦长最小时
相交,求相交弦长最小时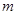 的值.
的值.
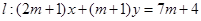 ,圆
,圆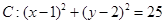
(1)判断直线
 和圆
和圆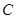 的位置关系;
的位置关系;(2)若直线
 和圆
和圆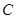 相交,求相交弦长最小时
相交,求相交弦长最小时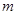 的值.
的值.(1)直线 和圆
和圆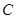 相交;(2)
相交;(2)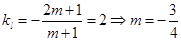 。
。
 和圆
和圆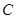 相交;(2)
相交;(2)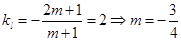 。
。本试题主要是考查了直线与圆的位置关系综合运用。
(1)因为利用圆心到直线的距离与圆的半径的关系,来确定结论。
(2)假设直线 和圆
和圆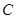 相交于点
相交于点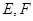 ,由相交弦长公式
,由相交弦长公式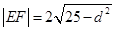 ,其中
,其中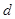 为圆心
为圆心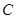 到直线
到直线 的距离,根据d的最大时的情况得到结论。
的距离,根据d的最大时的情况得到结论。
解:(1)直线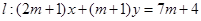 ,
,
即为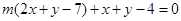 ,
,
则直线 经过直线
经过直线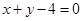 与
与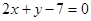 的交点
的交点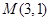
而 ,所以点
,所以点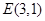 在圆
在圆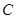 的内部,所以直线
的内部,所以直线 和圆
和圆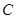 相交;
相交;
(2)假设直线 和圆
和圆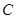 相交于点
相交于点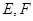 ,由相交弦长公式
,由相交弦长公式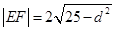 ,其中
,其中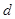 为圆心
为圆心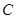 到直线
到直线 的距离,有公式可知,
的距离,有公式可知,
当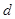 最大时,相交弦长最小,而由(1)知,
最大时,相交弦长最小,而由(1)知,
直线 过定点
过定点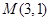 ,所以
,所以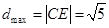 ,即
,即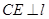 ,又
,又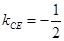 ,所以,
,所以,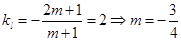
(1)因为利用圆心到直线的距离与圆的半径的关系,来确定结论。
(2)假设直线
 和圆
和圆 相交于点
相交于点 ,由相交弦长公式
,由相交弦长公式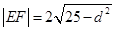 ,其中
,其中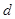 为圆心
为圆心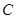 到直线
到直线 的距离,根据d的最大时的情况得到结论。
的距离,根据d的最大时的情况得到结论。解:(1)直线
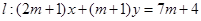 ,
,即为
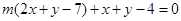 ,
,则直线
 经过直线
经过直线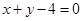 与
与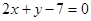 的交点
的交点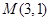
而
 ,所以点
,所以点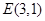 在圆
在圆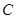 的内部,所以直线
的内部,所以直线 和圆
和圆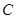 相交;
相交;(2)假设直线
 和圆
和圆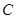 相交于点
相交于点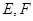 ,由相交弦长公式
,由相交弦长公式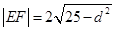 ,其中
,其中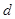 为圆心
为圆心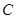 到直线
到直线 的距离,有公式可知,
的距离,有公式可知,当
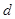 最大时,相交弦长最小,而由(1)知,
最大时,相交弦长最小,而由(1)知,直线
 过定点
过定点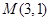 ,所以
,所以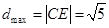 ,即
,即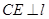 ,又
,又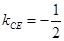 ,所以,
,所以,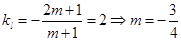

练习册系列答案
相关题目
 是直角三角形的三边(
是直角三角形的三边( 为斜边), 则圆
为斜边), 则圆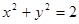 被直线
被直线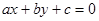 所截得的弦长等于__________.
所截得的弦长等于__________.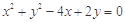 关于直线
关于直线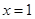 对称的圆的标准方程是____________.
对称的圆的标准方程是____________.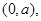 其斜率为1,且与圆
其斜率为1,且与圆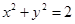 相切,则
相切,则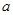 的值为
的值为 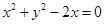 上的动点
上的动点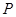 到直线
到直线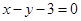 的最短距离为
的最短距离为 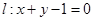 上有且仅有三个点到圆
上有且仅有三个点到圆 的距离为2;
的距离为2; 是圆
是圆 上的任意一点,动点
上的任意一点,动点 分
分 (
( 为坐标原点)的比为
为坐标原点)的比为 ,那么
,那么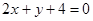 和圆
和圆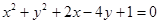 的交点,且满足下列条件之一的圆的方程. (1)过原点; (2)有最小面积.
的交点,且满足下列条件之一的圆的方程. (1)过原点; (2)有最小面积.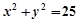 ,
, 内接于此圆,
内接于此圆, 点的坐标
点的坐标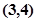 ,
,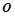 为坐标原点.
为坐标原点.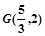 ,求直线
,求直线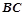 的方程;
的方程;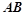 与直线
与直线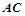 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线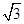 ),且斜率为1,求l与C相交所得的弦长.
),且斜率为1,求l与C相交所得的弦长.