题目内容
【题目】在等腰梯形ABCD中，AB∥DC，AB＝2，BC＝1，∠ABC＝60°．动点E和F分别在线段BC和DC上，且
．
（1）当λ
，求|
|；
（2）求
的最小值．
【答案】（1）
（2）
【解析】
以等腰梯形
的底
所在的直线为
轴，以的垂直平分线为
轴，建立如图所示的坐标系，根据向量的坐标运算求出
，
，
（1）当
时，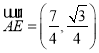
，即可求出答案；
（2）根据向量的数量积和基本不等式即可求出答案.
以等腰梯形ABCD的底AB所在的直线为x轴，以AB的垂直平分线为y轴，建立如图所示的坐标系，
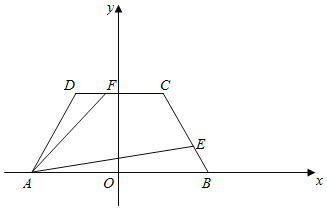
∵AB∥DC，AB＝2，BC＝1，∠ABC＝60°，
∴A（﹣1，0），B（1，0），C（
，
），D（
，），
∴
（2，0）+λ（，）=2λ，λ），
（1）当λ
时，
（
，
），则||
（2）∵
（，）
（1，0）＝（
，），
∴
2
，当且仅当λ
时取得最小值．
练习册系列答案
相关题目
【题目】2017年某市有2万多文科考生参加高考，除去成绩为670分（含670分）以上的3人与成绩为350分（不含350分）以下的3836人，还有约1．9万文科考生的成绩集中在
内，其成绩的频率分布如下表所示：
分数段 |
|
|
|
|
频率 |
|
|
|
|
分数段 |
|
|
|
|
频率 |
|
|
|
|
（1）试估计该次高考成绩在内文科考生的平均分（精确到
）；
（2）一考生填报志愿后，得知另外有4名同分数考生也填报了该志愿．若该志愿计划录取3人，并在同分数考生中随机录取，求该考生不被该志愿录取的概率．
