题目内容
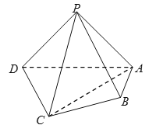
【题目】在三棱锥P﹣ABC中,PA⊥平面ABC,△ABC是边长为2的等边三角形,且三棱锥P﹣ABC的外接球表面积为![]() ,则直线PC与平面PAB所成角的正切值为_____.
,则直线PC与平面PAB所成角的正切值为_____.
【答案】![]()
【解析】
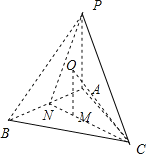
设三棱锥外接球的球心为O,半径为R,求出R,设M为△ABC的中心,N为AB的中点,
求出OM的长,再证明∠NPC就是直线PC与平面PAB所成角,利用直角三角函数求解.
设三棱锥外接球的球心为O,半径为R,
则S球=4πR2![]() ,故R
,故R![]() ,
,
设M为△ABC的中心,N为AB的中点,
则OM⊥平面ABC,且OC![]() ,NC
,NC![]() ,MC
,MC![]() ,
,
∴OM![]() 2,
2,
∵PA⊥平面ABC,故PA=2OM=4,∴PN![]() ,且PA⊥CN,又CN⊥AB,AB∩PA=A,
,且PA⊥CN,又CN⊥AB,AB∩PA=A,
∴CN⊥平面PAB,
所以∠NPC就是直线PC与平面PAB所成角.
∴tan∠NPC![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校高一年级共有![]() 名学生,其中男生
名学生,其中男生![]() 名,女生
名,女生![]() 名,该校组织了一次口语模拟考试(满分为
名,该校组织了一次口语模拟考试(满分为![]() 分).为研究这次口语考试成绩为高分是否与性别有关,现按性别采用分层抽样抽取
分).为研究这次口语考试成绩为高分是否与性别有关,现按性别采用分层抽样抽取![]() 名学生的成绩,按从低到高分成
名学生的成绩,按从低到高分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,并绘制成如图所示的频率分布直方图.已知
七组,并绘制成如图所示的频率分布直方图.已知![]() 的频率等于
的频率等于![]() 的频率,
的频率,![]() 的频率与
的频率与![]() 的频率之比为
的频率之比为![]() ,成绩高于
,成绩高于![]() 分的为“高分”.
分的为“高分”.

(1)估计该校高一年级学生在口语考试中,成绩为“高分”的人数;
(2)请你根据已知条件将下列![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“该校高一年级学生在本次口语考试中成绩及格(
的把握认为“该校高一年级学生在本次口语考试中成绩及格(![]() 分以上(含
分以上(含![]() 分)为及格)与性别有关”?
分)为及格)与性别有关”?
口语成绩及格 | 口语成绩不及格 | 合计 | |
男生 |
|
| |
女生 |
|
| |
合计 |
|
附临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]() .
.