题目内容
【题目】已知椭圆![]() 的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,
的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,![]() 最大值为1.
最大值为1.
(1)求椭圆C的方程;
(2)不过点F2的直线l:y=kx+m(m≠0)交椭圆C于A,B两点.
①若![]() ,且
,且![]() ,求m的值.
,求m的值.
②若x轴上任意一点到直线AF2与BF2距离相等,求证:直线l过定点,并求出该定点的坐标.
【答案】(1)![]() .(2)①
.(2)①![]() ,②
,②![]() .
.
【解析】
(1)根据题意,可求得c=1,b=1,进而求得a,由此得到椭圆方程;
(2)①联立方程,得到k与m的不等关系,及两根的关系,表示出弦长AB及点O到直线AB的距离,由此建立等式解出即可;②依题意,k1+k2=0,由此可得到k与m的等量关系,进而求得定点.
解:(1)由抛物线的方程y2=4x得其焦点为(1,0),则c=1,
当点M为椭圆的短轴端点时,△MF1F2面积最大,此时![]() ,则b=1,
,则b=1,
∴![]() ,故椭圆的方程为
,故椭圆的方程为![]() ;
;
(2)联立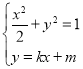 得,(1+2k2)x2+4kmx+2m2﹣2=0,
得,(1+2k2)x2+4kmx+2m2﹣2=0,
△=16k2m2﹣4(2k2+1)(2m2﹣2)=8(2k2﹣m2+1)>0,得1+2k2>m2(*),
设A(x1,y1),B(x2,y2),则![]() ,
,
①∵m≠0且![]() ,代入(*)得,0<m2<2,
,代入(*)得,0<m2<2,
![]() ,
,
设点O到直线AB的距离为d,则![]() ,
,
∴![]() ,
,
∴m2=1∈(0,2),则m=±1;
②![]() ,
,
由题意,k1+k2=0,
∴![]() ,即2kx1x2+(m﹣k)(x1+x2)﹣2m=0,
,即2kx1x2+(m﹣k)(x1+x2)﹣2m=0,
∴![]() ,
,
解得m=﹣2k,
∴直线l的方程为y=k(x﹣2),故直线l恒过定点,该定点坐标为(2,0).

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目