题目内容
【题目】设递增等比数列{an}的前n项和为Sn,且a2=3,S3=13,数列{bn}满足b1=a1,点P(bn,bn+1)在直线x﹣y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
【答案】(1)an=3n﹣1,bn=2n﹣1(2)Tn=3﹣(n+1)(![]() )n﹣1
)n﹣1
【解析】
(1)利用基本量法求解![]() ,再代入
,再代入![]() 到直线
到直线![]() 可得
可得![]() 为等差数列,再进行通项公式求解即可.
为等差数列,再进行通项公式求解即可.
(2)利用错位相减求和即可.
(1)递增等比数列{an}的公比设为q,前n项和为Sn,且a2=3,S3=13,
可得a1q=3,a1+a1q+a1q2=13,解得q=3或q![]() ,
,
由等比数列递增,可得q=3,a1=1,则![]() ;
;
P(bn,bn+1)在直线x﹣y+2=0上,可得bn+1﹣bn=2,
且b1=a1=1,则bn=1+2(n﹣1)=2n﹣1;
(2)cn![]() (2n﹣1)(
(2n﹣1)(![]() )n﹣1,
)n﹣1,
前n项和Tn=11+3![]() 5
5![]() (2n﹣1)(
(2n﹣1)(![]() )n﹣1,
)n﹣1,
![]() Tn=1
Tn=1![]() 3
3![]() 5
5![]() (2n﹣1)(
(2n﹣1)(![]() )n,
)n,
相减可得![]() Tn=1+2(
Tn=1+2(![]() (
(![]() )n﹣1)﹣(2n﹣1)(
)n﹣1)﹣(2n﹣1)(![]() )n
)n
=1+2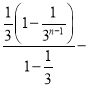 (2n﹣1)(
(2n﹣1)(![]() )n,
)n,
化简可得Tn=3﹣(n+1)(![]() )n﹣1.
)n﹣1.

练习册系列答案
相关题目