题目内容
【题目】已知函数f(x)=ln(x+1)+ ![]() .
.
(I)讨论函数f(x)在(0,+∞)上的单调性;
(II)设函数f(x)存在两个极值点,并记作x1 , x2 , 若f(x1)+f(x2)>4,求正数a的取值范围;
(III)求证:当a=1时,f(x)> ![]() (其中e为自然对数的底数)
(其中e为自然对数的底数)
【答案】解:(Ⅰ)  ,(*)
,(*)
当a≥2时,∵x>0,∴ 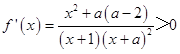 ,函数f(x)在(0,+∞)上是增函数;
,函数f(x)在(0,+∞)上是增函数;
当0<a<2时,由f'(x)=0,得x2+a(a﹣2)=0,解得 ![]() (负值舍去),
(负值舍去), ![]() ,
,
所以当x∈(0,x2)时,x2+a(a﹣2)<0,从而f'(x)<0,函数f(x)在(0,x2)上是减函数;
当x∈(x2,+∞)时,x2+a(a﹣2)>0,从而f'(x)>0,函数f(x)在(x2,+∞)上是增函数.
综上,当a≥2时,函数f(x)在(0,+∞)上是增函数;
当0<a<2时,函数f(x)在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数
上是增函数
(Ⅱ)由(Ⅰ)知,当a≥2时,f'(x)>0,函数f(x)无极值点;
要使函数f(x)存在两个极值点,必有0<a<2,且极值点必为 ![]() ,
, ![]() ,
,
又由函数定义域知,x>﹣1,则有 ![]() ,即
,即 ![]() ,化为(a﹣1)2>0,所以a≠1,
,化为(a﹣1)2>0,所以a≠1,
所以,函数f(x)存在两个极值点时,正数a的取值范围是(0,1)∪(1,2).
由(*)式可知, 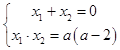 ,
,
f(x1)+f(x2)
=ln(1+x1)+ ![]() +ln(1+x2)+
+ln(1+x2)+ ![]()
=ln(1+x1+x2+x1x2)+ ![]()
=ln[(a﹣1)2]+ 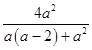
=ln[(a﹣1)2]+ ![]() ﹣2;
﹣2;
不等式f(x1)+f(x2)>4化为 ![]() ,
,
令a﹣1=t(a∈(0,1)∪(1,2)),所以t∈(﹣1,0)∪(0,1),
令 ![]() ,t∈(﹣1,0)∪(0,1).
,t∈(﹣1,0)∪(0,1).
当t∈(﹣1,0)时, ![]() ,
, ![]() ,所以g(t)<0,不合题意;
,所以g(t)<0,不合题意;
当t∈(0,1)时, ![]() ,
, ![]() ,
,
所以g(t)在(0,1)是减函数,所以 ![]() ,适合题意,即a∈(1,2).
,适合题意,即a∈(1,2).
综上,若f(x1)+f(x2)>4,此时正数a的取值范围是(1,2).
(Ⅲ)证明:当a=1时, ![]() ,
,
不等式 ![]() 可化为
可化为 ![]() ,所以
,所以
要证不等式 ![]() ,即证
,即证 ![]() ,即证
,即证 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
在(0,1)上,h'(x)<0,h(x)是减函数;
在¨1+∞)上,h'(x)>0,h(x)是增函数.
所以h(x)≥h(1)=1,
设 ![]() ,则(x)是减函数,
,则(x)是减函数,
所以(x)<(0)=1,
所以(x)<h(x),即 ![]() ,
,
所以当a=1时,不等式 ![]() 成立
成立
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;(Ⅱ)求出x1,x2,得到f(x1)+f(x2)的解析式,问题转化为 ![]() ,令a﹣1=t(a∈(0,1)∪(1,2)),所以t∈(﹣1,0)∪(0,1),令
,令a﹣1=t(a∈(0,1)∪(1,2)),所以t∈(﹣1,0)∪(0,1),令 ![]() ,根据函数的单调性判断即可;(Ⅲ)问题转化为证明
,根据函数的单调性判断即可;(Ⅲ)问题转化为证明 ![]() ,即证
,即证 ![]() ,设
,设 ![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的极值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

【题目】某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表: A型车挖掘机
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车挖掘机
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅰ)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(Ⅱ)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
