题目内容
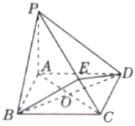
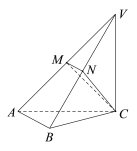
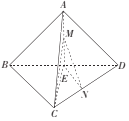
【题目】如图，在三棱锥A﹣BCD中，点E在BD上，EA＝EB＝EC＝ED，BD
CD，△ACD为正三角形，点M，N分别在AE，CD上运动（不含端点），且AM＝CN，则当四面体C﹣EMN的体积取得最大值
时，三棱锥A﹣BCD的外接球的表面积为_____.
【答案】32π
【解析】
设ED＝a，根据勾股定理的逆定理可以通过计算可以证明出CE⊥ED. AM＝x，根据三棱锥的体积公式，运用基本不等式，可以求出AM的长度，最后根据球的表面积公式进行求解即可.
设ED＝a，则CD
a.可得CE2+DE2＝CD2，∴CE⊥ED.
当平面ABD⊥平面BCD时，当四面体C﹣EMN的体积才有可能取得最大值，设AM＝x.
则四面体C﹣EMN的体积
（a﹣x）
a×x
ax（a﹣x）
，当且仅当x
时取等号.
解得a＝2
.
此时三棱锥A﹣BCD的外接球的表面积＝4πa2＝32π.
故答案为：32π
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】为了政府对过热的房地产市场进行调控决策，统计部门对城市人和农村人进行了买房的心理预期调研，用简单随机抽样的方法抽取110人进行统计，得到如下列联表：
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3：8．
分别求样本中城市人中的不买房人数和农村人中的纠结人数；
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关？
参考公式：
．
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
