题目内容
【题目】为了政府对过热的房地产市场进行调控决策，统计部门对城市人和农村人进行了买房的心理预期调研，用简单随机抽样的方法抽取110人进行统计，得到如下列联表：
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3：8．
分别求样本中城市人中的不买房人数和农村人中的纠结人数；
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关？
参考公式：
．
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
【答案】（1）样本中城市人中的不买房人数为10人，农村人中的纠结人数为50人；（2）有
的把握认为不买房与城乡有关.
【解析】
设城市人中的不买房人数为x，农村人中的纠结人数为y，根据题意列出方程组求解即可；
设三种心理障碍都与性别无关，由得到列联表，对于上述三种心理障碍分别构造三个随机变量
，
，
；由表中数据计算、和的值，对照数表得出结论．
解：设城市人中的不买房人数为x，农村人中的纠结人数为y，
则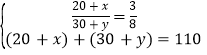
，
解得
；
样本中城市人中的不买房人数为10人，农村人中的纠结人数为50人；
设三种心理障碍都与性别无关，由得到列联表如下；
买房 | 不买房 | 纠结 | 总计 | |
城市人 | 5 | 10 | 15 | 30 |
农村人 | 20 | 10 | 50 | 85 |
总计 | 25 | 20 | 65 | 110 |
对于上述三种心理障碍分别构造三个随机变量，，；
由表中数据可得
；
；
；
所以，没有充分的证明显示买房与城乡有关，
有的把握认为不买房与城乡有关，
没有充分的证明显示纠结与城乡有关．
期末冲刺100分创新金卷完全试卷系列答案【题目】已知某校5个学生的数学和物理成绩如下：
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学成绩 | 80 | 75 | 70 | 65 | 60 |
物理成绩 | 70 | 66 | 68 | 64 | 62 |
（1）通过大量事实证明发现，一个学生的数学成绩和物理成绩是具有很强的线性相关关系的，在上述表格中，用
表示数学成绩，用
表示物理成绩，求关于的回归方程．
（2）利用残差分析回归方程的拟合效果，若残差和在
范围内，则称回归方程为“优拟方程”，问：该回归方程是否为“优拟方程”．
（3）现从5名同学中任选两人参加访谈活动，求1号同学没被选中的概率.
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：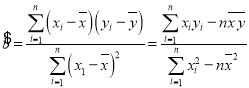
，
.
