题目内容
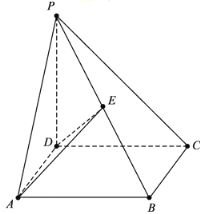
【题目】如图，在四棱锥
中，ABCD为菱形，
平面ABCD，连接AC，BD交于点O，
，
，E是棱PC上的动点，连接DE.
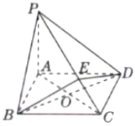
（1）求证：平面
平面
；
（2）当
面积的最小值是4时，求此时点E到底面ABCD的距离.
【答案】（1）证明见解析；（2）
.
【解析】
（1）由题意可证得
，
，从而可得
平面PAC，再由面面垂直的判定定理即可证出.
（2）连接OE，由（1）可得
，
面积的最小值是4时，可求出
，作
交AC于H，可知
平面ABCD， 由
即可求解.
（1）证明：∵四边形ABCD是菱形，∴.
∵
平面ABCD，
平面ABCD，
∴.
又
，∴平面PAC.
又平面BDE，
∴平面
平面PAC.
（2）解：如图（1），连接OE，由（1）知平面PAC，
平面PAC.
∴.
∵
，由
，得
.
∵当
时，OE取到最小值1.此时
.
作交AC于H，∵平面ABCD，∴平面ABCD，
如图（2），由
，得点E到底面ABCD的距离
.
（1） （2）
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某语文报社为研究学生课外阅读时间与语文考试中的作文分数的关系，随机调查了本市某中学高三文科班
名学生每周课外阅读时间
（单位：小时）与高三下学期期末考试中语文作文分数
，数据如下表：
| 1 | 2 | 3 | 4 | 5 | 6 |
| 38 | 40 | 43 | 45 | 50 | 54 |
（1）根据上述数据，求出高三学生语文作文分数与该学生每周课外阅读时间的线性回归方程，并预测某学生每周课外阅读时间为
小时时其语文作文成绩；
（2）从这人中任选
人，这人中至少有
人课外阅读时间不低于
小时的概率.
参考公式：
，其中
，
参考数据：
，
，
