Question

【题目】在平面直角坐标系xOy中，已知椭圆1（a＞b＞0）的焦距F1F2的长为2，经过第二象限内一点P（m，n）的直线1与圆x2+y2＝a2交于A，B两点，且OA．

（1）求PF1+PF2的值；

（2）若，求m，n的值．

Answer 1

【答案】（1）2．（2）m＝﹣1，n．

【解析】

（1）先说明点P在椭圆上，根据椭圆性质即可得解；

（2）设A（x1，y1），B（x2，y2），联立方程组得x1+x2，x1x2，转化条件得x2﹣x1，代入解方程即可得解.

（1）∵OA，∴a．

∵把点P（m，n）代入直线方程1，可得：1，

∴点P在椭圆上，

∴PF1+PF2＝2a＝2．

（2）由a，c＝1，∴b2＝a2﹣c2＝1．

设A（x1，y1），B（x2，y2）．

联立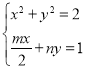，化为：（4n2+m2）x2﹣4mx+4﹣8n2＝0，

∴x1+x2，x1x2．

∵，∴（x2﹣x1，y2﹣y1）（2，0），

化为2（x2﹣x1），即x2﹣x1，

∴4x1x2，

代入可得：，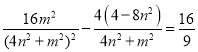

化为：56n4+10n2m2﹣36n2﹣m4＝0，

又1，

把m2＝2﹣2n2代入化为8n4﹣2n2﹣1＝0，

解得m2＝1，n2．

∵点P在第二象限，

∴取m＝﹣1，n．