Question

【题目】已知函数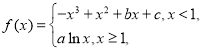图象过点，且在该点处的切线与直线垂直．

（1）求实数，的值；

（2）对任意给定的正实数，曲线上是否存在两点，，使得是以为直角顶点的直角三角形，且此三角形斜边中点在轴上？

Answer 1

【答案】（1）；（2）存在，理由见解析．

【解析】

试题分析：（1）首先求得导函数，然后根据导数的几何意义得到关于的方程组，从而求解即可；（2）首先假设曲线上存在两点，，使得是以为直角顶点的直角三角形，从而根据条件设出的坐标，然后根据向量垂直的充要条件建立方程，再根据方程解的情况构造新函数，从而通过求导研究新函数的单调性，进而得出结论．

试题解析：（1）当时，，则，

由题意知解得．

（2）假设曲线上存在两点，，使得是以为直角顶点的直角三角形，则，只能在轴的两侧，不妨设（），则，且．

因为是以为直角顶点的直角三角形，所以，

即，（1）

是否存在点，等价于方程（1）是否有解，

若，则，代入方程（1）得：，此方程无实数解．

若，则，代入方程（1）得到，

设，则在上恒成立，

所以在上单调递增，从而，

所以当时，方程有解，即方程（1）有解，

所以对任意给定的正实数，曲线上存在两点，，使得是以为直角顶点的直角三角形，且此三角形斜边中点在轴上．