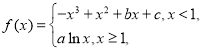题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() ….
….
(Ⅰ)判断函数![]() 的单调性,并说明理由;
的单调性,并说明理由;
(Ⅱ)若![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)理由见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)首先求出导函数,然后分![]() 、
、![]() 求得函数的单调区间;(Ⅱ)首先将问题转化为
求得函数的单调区间;(Ⅱ)首先将问题转化为![]() ,
,![]() 恒成立,由此令
恒成立,由此令![]() ,然后通过求导研究其单调性并求得其最大值,从而求得
,然后通过求导研究其单调性并求得其最大值,从而求得![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由题可知,![]() ,则
,则![]() ,
,
(i)当![]() 时,
时,![]() ,函数
,函数![]() 为
为![]() 上的减函数,
上的减函数,
(ii)当![]() 时,令
时,令![]() ,得
,得![]() ,
,
①若![]() ,则
,则![]() ,此时函数
,此时函数![]() 为单调递减函数;
为单调递减函数;
②若![]() ,则
,则![]() ,此时函数
,此时函数![]() 为单调递增函数.
为单调递增函数.
(Ⅱ)由题意,问题等价于![]() ,不等式
,不等式![]() 恒成立,
恒成立,
即![]() ,
,![]() 恒成立,
恒成立,
令![]() ,则问题等价于
,则问题等价于![]() 不小于函数
不小于函数![]() 在
在![]() 上的最大值.
上的最大值.
由![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 的最大值为
的最大值为![]() ,
,
故![]() ,不等式
,不等式![]() 恒成立,实数
恒成立,实数![]() 的取值范围为
的取值范围为![]() .
.

 阅读快车系列答案
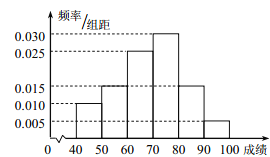
阅读快车系列答案【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
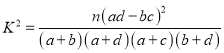 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
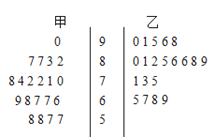
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写![]() 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式与临界值表: 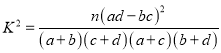 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |