题目内容
11.设集合A={(x,y)|(x-3)2+(y-4)2=$\frac{4}{5}$},B={(x,y)|(x-3)2+(y-4)2=$\frac{16}{5}$},C={(x,y)|2|x-3|+|y-4|=λ},若(A∪B)∩C≠∅,则实数λ的取值范围是[$\frac{2\sqrt{5}}{5}$,4].
分析 集合A,B表示以(3,4)点为圆心,半径分别为$\frac{2\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$的圆,集合C在λ>0时,表示以(3,4)为中心,四条边的斜率为±2的菱形,若(A∪B)∩C≠∅,则菱形与A或B圆有交点,进而可得实数λ的取值范围.
解答 解:集合A={(x,y)|(x-3)2+(y-4)2=$\frac{4}{5}$}表示以(3,4)点为圆心半径为$\frac{2\sqrt{5}}{5}$的圆,
集合B={(x,y)|(x-3)2+(y-4)2=$\frac{16}{5}$}表示以(3,4)点为圆心半径为$\frac{4\sqrt{5}}{5}$的圆,
集合C={(x,y)|2|x-3|+|y-4|=λ}在λ>0时,表示以(3,4)为中心,四条边的斜率为±2的菱形,
如下图所示: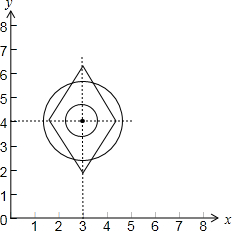
若(A∪B)∩C≠∅,则菱形与A或B圆有交点,
当λ<$\frac{2\sqrt{5}}{5}$时,菱形在小圆的内部,与两圆均无交点,不满足答案;
当菱形与大圆相切时,圆心(3,4)到菱形2|x-3|+|y-4|=λ任一边的距离等于大于半径$\frac{4\sqrt{5}}{5}$,
当x>3,且y>4时,菱形一边的方程可化为2x+y-(10+λ)=0,
由d=$\frac{|10-(10+λ)|}{\sqrt{5}}=\frac{4\sqrt{5}}{5}$得:λ=4,
故λ>4时,两圆均在菱形内部,与菱形无交点,不满足答案;
综上实数λ的取值范围是($\frac{2\sqrt{5}}{5}$,4],
故答案为:[$\frac{2\sqrt{5}}{5}$,4]
点评 本题考查的知识点是集合的交集,并集,补集运算,熟练掌握并正确理解集合运算的定义是解答的关键.

| A. | y=x3 | B. | y=$\sqrt{x}$ | C. | y=cosx | D. | y=2|x| |
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{{2}^{2014}}$ | C. | $\frac{1}{2015}$ | D. | $\frac{1}{{2}^{2015}}$ |
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$ | C. | xy=±2$\sqrt{2}$x | D. | y=±$\sqrt{11}$x |