题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其短轴的两个端点与长轴的一个端点构成的三角形的面积为
,其短轴的两个端点与长轴的一个端点构成的三角形的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与圆
与圆![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 和
和![]() ,若
,若![]() 为坐标原点),求线段
为坐标原点),求线段![]() 长度的取值范围.
长度的取值范围.
【答案】(1)![]() ;(2)
;(2)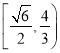 .
.
【解析】
(1)椭圆的离心率和其短轴的两个端点与长轴的一个端点构成的三角形的面积,得![]() ,
,![]() ,
,![]() 方程组求解,即可写出椭圆方程.
方程组求解,即可写出椭圆方程.
(2)直线与圆![]() 相切得
相切得![]() ,
,![]() ,再联立直线和椭圆,得到关于
,再联立直线和椭圆,得到关于![]() 的一元二次方程,利用由韦达定理分别得到
的一元二次方程,利用由韦达定理分别得到![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数,再求取值范围.
的函数,再求取值范围.
(1)![]() 椭圆的离心率为
椭圆的离心率为![]() ,
,
![]() ,即
,即![]() ,①
,①
又![]() 其短轴的两个端点与长轴的一个端点构成的三角形的面积为
其短轴的两个端点与长轴的一个端点构成的三角形的面积为![]() .
.
![]()
![]() ,即
,即![]() ,②
,②
![]() ,③
,③
由①②③得![]() ,
,![]() ,
,![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
(2)![]() 直线
直线![]() 与圆
与圆![]() 相切,
相切,
![]()
![]() ,即
,即![]() ,
,![]()
![]() 直线
直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 和
和![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立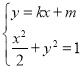 ,得
,得![]() ,
,
△![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
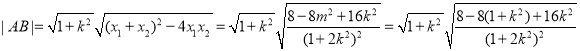
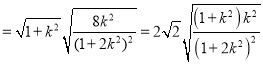 ,,
,,
又因为![]() ,
,
把上面![]() 代入上式,得,
代入上式,得,
![]() ,又
,又![]()
![]() ,
,
![]()
![]() ,∴
,∴![]() ,
,
令![]() 则
则![]() ,
,![]() ,所以
,所以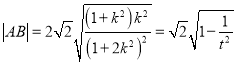 ,
,
![]() 线段
线段![]() 长度的取值范围
长度的取值范围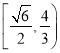 .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目