题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过
经过![]() ,
,![]() ,
,![]() 三点,
三点,![]() 是线段
是线段![]() 上的动点,
上的动点,![]() ,
,![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 是使
是使![]() 恒成立的最小正整数.
恒成立的最小正整数.
①求![]() 的值;
的值;
②求三角形![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)确定出圆的圆心坐标,然后考虑直线![]() 的斜率是否存在,斜率存在时利用半弦长、半径、圆心到直线的距离构造成的直角三角形求解出直线的方程,注意验证是否符合;
的斜率是否存在,斜率存在时利用半弦长、半径、圆心到直线的距离构造成的直角三角形求解出直线的方程,注意验证是否符合;
(2) ①根据![]() 得到
得到![]() 的轨迹应该满足的条件,再将其转化为点到直线距离问题完成求解;
的轨迹应该满足的条件,再将其转化为点到直线距离问题完成求解;
②考虑分类讨论直线的斜率存在与否,并计算或表示出对应的面积,从而确定出面积的最小值.
(1)由题意可知,圆![]() 的直径为
的直径为![]() ,
,
所以圆![]() 方程为:
方程为:![]() .
.
因为![]() ,所以
,所以![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
若![]() 斜率不存在,则
斜率不存在,则![]() 到直线
到直线![]() 的距离为2,不符合,所以
的距离为2,不符合,所以![]() 斜率存在;
斜率存在;
设![]() 方程为:
方程为:![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,直线
时,直线![]() 与
与![]() 轴无交点,不符合,舍去.
轴无交点,不符合,舍去.
所以![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
(2)①设![]() ,由点
,由点![]() 在线段
在线段![]() 上,得
上,得![]() ,即
,即![]() .
.
由![]() ,得
,得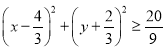 .
.
依题意知,线段![]() 与圆
与圆 至多有一个公共点,
至多有一个公共点,
故 ,解得
,解得![]() 或
或![]() .
.
因为![]() 是使
是使![]() 恒成立的最小正整数,所以
恒成立的最小正整数,所以![]() .
.
②![]() ,圆
,圆![]() 方程为:
方程为:![]() ,
,
(i)当直线![]() :
:![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,此时,
,此时,![]() ;
;
(ii)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为:
的方程为:![]() ,
,
则![]() 的方程为:
的方程为:![]() ,点
,点![]() .所以,
.所以,![]() .
.
又圆心![]() 到
到![]() 的距离为
的距离为![]() ,
,
所以, .
.
故![]()
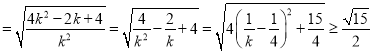 ,取等号时
,取等号时![]() .
.
又因为![]() ,所以三角形
,所以三角形![]() 面积的最小值为
面积的最小值为![]() .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标.
分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的.报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分.若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分.
在某次招标中,若基准价为1000(万元).甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 | A甲分 |
乙 | 70分 | 100分 | A乙分 |
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是( )
A. 73,75.4B. 73,80C. 74.6,76D. 74.6,75.4