题目内容
12. 如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )
如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
分析 设点A在面BCD内的射影为A′,由三棱锥A-BCD为正三棱锥,易得A′为△BCD中心,由线面垂直的判定定理可得AB⊥面ACD,即∠ADB为直线BD与平面ACD所成角,解三角形ADB可得直线BD与平面ACD所成的角,即可求出点B到平面ACD的距离.
解答 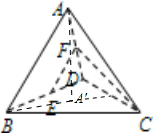 解:设点A在面BCD内的射影为A′,
解:设点A在面BCD内的射影为A′,
∵三棱锥A-BCD为正三棱锥,
∴AB=AD,
△BCD为正三角形,A′为△BCD中心,
∴CD⊥BA′,
∵AA′⊥面BCD,
∴CD⊥AB,
∵E、F分别为BD、AD的中点,∴EF∥AB,
∵EF⊥CF,∴AB⊥CF,
又∵AB⊥CD,CD∩CF=C,
∴AB⊥面ACD,
∴AB⊥AD.
∴∠ADB即为直线BD与平面ACD所成角,
又∵AB=AD,AB⊥AD,
∴∠ADB=45°,
∴直线BD与平面ACD所成角为45°,
∵BD=2,
∴点B到平面ACD的距离为2sin45°=$\sqrt{2}$.
故选:D.
点评 本题考查点B到平面ACD的距离,考查直线与平面所成的角,其中求出∠ADB为直线BD与平面ACD所成角是解答的关键.

练习册系列答案
相关题目
1.已知椭圆C:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1的右焦点为F,定点A(4,1),P是椭圆C上的动点,则|PA|+|PF|的取值范围是( )
| A. | [10-$\sqrt{65}$,10+$\sqrt{65}$] | B. | [2,18] | C. | [$\frac{13}{5}$,9+$\sqrt{82}$] | D. | [10-$\sqrt{65}$,10] |
12.如图所示,PA=PB=PC,且它们所成的角均为60°,则二面角B-PA-C的余弦值是( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1. 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.