题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且(2a+c)·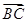 ·
·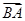 +c
+c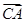 ·
·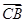 =0.
=0.
(1)求角B的大小;
(2)若b=2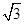 ,试求
,试求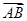 ·
·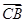 的最小值.
的最小值.
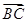 ·
·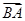 +c
+c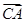 ·
·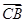 =0.
=0.(1)求角B的大小;
(2)若b=2
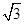 ,试求
,试求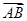 ·
·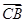 的最小值.
的最小值.(1)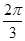 (2)-2
(2)-2
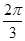 (2)-2
(2)-2(1)因为(2a+c)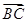 ·
·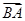 +c
+c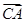 ·
·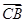 =0,
=0,
所以(2a+c)accosB+abccosC=0,
即(2a+c)cosB+bcosC=0,
所以(2sinA+sinC)cosB+sinBcosC=0,
即2sinAcosB+sin(B+C)=0.
因为sin(B+C)=sinA≠0,
所以cosB=-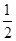 ,所以B=
,所以B=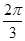 .
.
(2)因为b2=a2+c2-2accos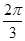 ,所以12=a2+c2+ac≥3ac,即ac≤4,
,所以12=a2+c2+ac≥3ac,即ac≤4,
所以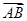 ·
·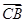 =accos
=accos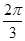 =-
=-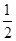 ac≥-2,当且仅当a=c=2时等号成立,
ac≥-2,当且仅当a=c=2时等号成立,
所以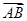 ·
·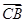 的最小值为-2.
的最小值为-2.
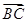 ·
·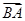 +c
+c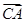 ·
·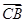 =0,
=0,所以(2a+c)accosB+abccosC=0,
即(2a+c)cosB+bcosC=0,
所以(2sinA+sinC)cosB+sinBcosC=0,
即2sinAcosB+sin(B+C)=0.
因为sin(B+C)=sinA≠0,
所以cosB=-
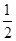 ,所以B=
,所以B=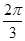 .
.(2)因为b2=a2+c2-2accos
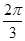 ,所以12=a2+c2+ac≥3ac,即ac≤4,
,所以12=a2+c2+ac≥3ac,即ac≤4,所以
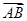 ·
·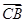 =accos
=accos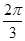 =-
=-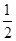 ac≥-2,当且仅当a=c=2时等号成立,
ac≥-2,当且仅当a=c=2时等号成立,所以
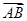 ·
·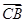 的最小值为-2.
的最小值为-2.
练习册系列答案
相关题目
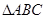 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.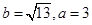 ,求边c的值;
,求边c的值;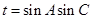 ,求t的最大值.
,求t的最大值.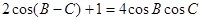
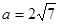 ,△ABC的面积为
,△ABC的面积为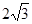 ,求
,求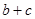 .
.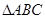 中,
中,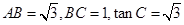 ,则
,则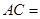 ______.
______.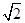 的等比数列,则其最大角的余弦值为________.
的等比数列,则其最大角的余弦值为________.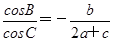 .
.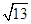 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.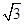 ),n=
),n=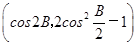 ,且m∥n
,且m∥n