题目内容
在△ABC中,a、b、c分别是角A、B、C的对边,且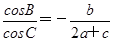 .
.
(1)求角B的大小;
(2)若b=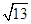 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
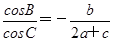 .
.(1)求角B的大小;
(2)若b=
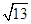 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.(1)B=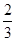 π(2)
π(2)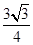
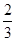 π(2)
π(2)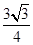
(1)由余弦定理知:cosB=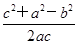 ,
,
cosC=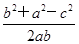 .将上式代入
.将上式代入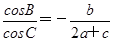 ,得
,得
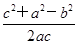 ·
·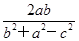 =-
=-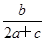 ,
,
整理得a2+c2-b2=-ac.∴cosB=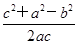 =-
=-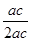 =-
=-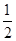 .
.
∵B为三角形的内角,∴B=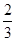 π.
π.
(2)将b=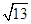 ,a+c=4,B=
,a+c=4,B=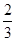 π代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB,
π代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB,
∴13=16-2ac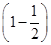 ,∴ac=3.
,∴ac=3.
∴S△ABC=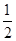 acsinB=
acsinB=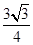 .
.
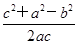 ,
,cosC=
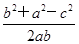 .将上式代入
.将上式代入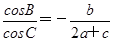 ,得
,得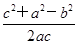 ·
·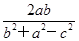 =-
=-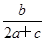 ,
,整理得a2+c2-b2=-ac.∴cosB=
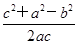 =-
=-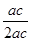 =-
=-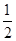 .
.∵B为三角形的内角,∴B=
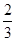 π.
π.(2)将b=
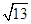 ,a+c=4,B=
,a+c=4,B=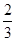 π代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB,
π代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB,∴13=16-2ac
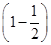 ,∴ac=3.
,∴ac=3.∴S△ABC=
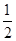 acsinB=
acsinB=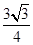 .
.
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 中,
中, 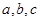 分别是角
分别是角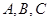 的对边,且
的对边,且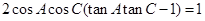 .
. 的大小; (2)若
的大小; (2)若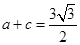 ,
,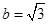 ,求
,求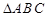 中,角
中,角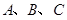 所对的边分别为
所对的边分别为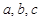 ,且
,且 ,
, ,求
,求 的取值范围.
的取值范围.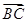 ·
·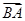 +c
+c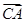 ·
·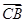 =0.
=0.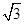 ,试求
,试求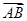 ·
·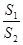 的最小值.
的最小值.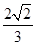 ,AB=3
,AB=3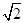 ,AD=3,则BD的长为________.
,AD=3,则BD的长为________.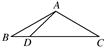
 中,角
中,角 所对的边分别为
所对的边分别为 .若
.若 ,
, ,
,

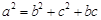 ,则A等于 ( )
,则A等于 ( )