题目内容
已知定义在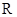 上的函数
上的函数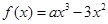 ,其中
,其中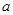 为大于零的常数.
为大于零的常数.
(Ⅰ)当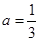 时,令
时,令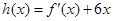 ,求证:当
,求证:当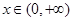 时,
时,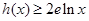 (
(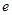 为自然对数的底数);
为自然对数的底数);
(Ⅱ)若函数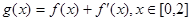 ,在
,在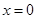 处取得最大值,求
处取得最大值,求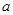 的取值范围.
的取值范围.
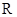 上的函数
上的函数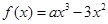 ,其中
,其中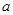 为大于零的常数.
为大于零的常数.(Ⅰ)当
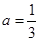 时,令
时,令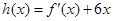 ,求证:当
,求证:当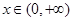 时,
时,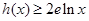 (
(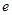 为自然对数的底数);
为自然对数的底数);(Ⅱ)若函数
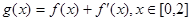 ,在
,在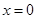 处取得最大值,求
处取得最大值,求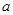 的取值范围.
的取值范围.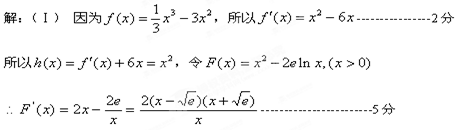
所以
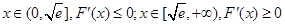
所以当
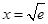 时,
时,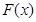 取得极小值,
取得极小值,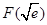 为
为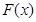 在
在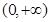 上的最小值
上的最小值因为
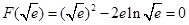
所以
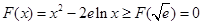 ,即
,即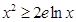 -------------------6分
-------------------6分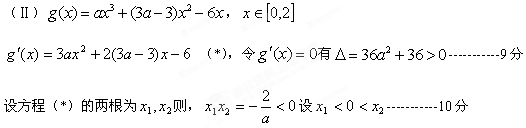
当
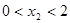 时,
时,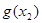 为极小值,所以
为极小值,所以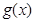 在[0,2]上的最大值只能为
在[0,2]上的最大值只能为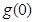 或
或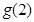 ;
;当
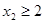 时,
时,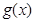 在
在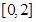 上单调递减,最大值为
上单调递减,最大值为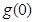 ,
,所以
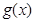 在
在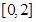 上的最大值只能为
上的最大值只能为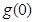 或
或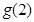 ; -------------------11分
; -------------------11分又已知
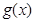 在
在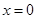 处取得最大值,所以
处取得最大值,所以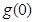
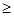
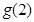
即
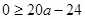 解得
解得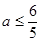 ,所以
,所以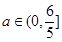 ---------------13分
---------------13分略

练习册系列答案
相关题目
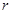 (单位:米)与时间
(单位:米)与时间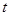 (单位:秒)的函数关系是
(单位:秒)的函数关系是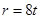 ,则在2秒末扰动水面面积的变化率为( )
,则在2秒末扰动水面面积的变化率为( )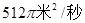
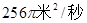
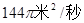
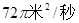
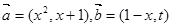 ,若函数
,若函数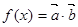 在区间
在区间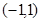 上是增函数,求
上是增函数,求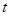 的取值范围。
的取值范围。 到底面中心
到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
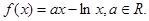
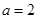 时,求曲线
时,求曲线 在点
在点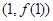 处的切线方程;
处的切线方程;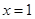 处有极值,求
处有极值,求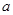 ,使
,使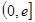 的最小值是3,若存在,求出
的最小值是3,若存在,求出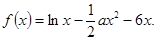
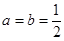 时,求函数
时,求函数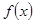 的单调区间;
的单调区间;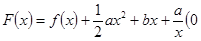 <
<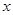 ≤
≤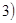 ,其图像上任意一点P
,其图像上任意一点P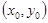 处切线的斜率
处切线的斜率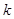 ≤
≤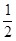 恒成立,求实数
恒成立,求实数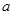 的取值范围;
的取值范围;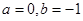 时,方程
时,方程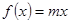 在区间
在区间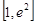 内有唯一实数解,求实数
内有唯一实数解,求实数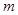 的取值范围。
的取值范围。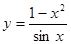 ,则
,则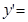 ( ).
( ).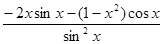
 (单位:N)的的作用下,沿着与力F相同的方向,从
(单位:N)的的作用下,沿着与力F相同的方向,从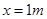 处运动到
处运动到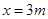 处, 则力
处, 则力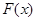 所作的功为( )
所作的功为( )