题目内容
请你设计一顶帐篷,它下部的形状是高为1m的正棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示),试问当帐篷的顶点 到底面中心
到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?

 到底面中心
到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
解:设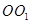 为
为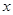 m,则1<x<4.
m,则1<x<4.
由题设可得正六棱锥底面边长为(单位:m)
 …………………2分
…………………2分
于是底面正六边形的面积为(单位:m2)
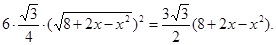 …………………4分
…………………4分
帐篷的体积为(单位:m3)
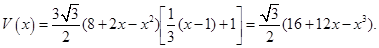 ……………6分
……………6分
求导数,得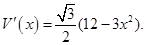 ………………8分
………………8分
令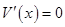 ,解得x=-2(不合题意,舍去),x=2.
,解得x=-2(不合题意,舍去),x=2.
当1<x<2时,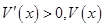 为增函数;当2<x<4时,
为增函数;当2<x<4时,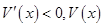 为减函数.
为减函数.
所以当x=2时,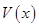 最大. …………………11分
最大. …………………11分
答:当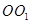 为2m时,帐篷的体积最大. …………………12分
为2m时,帐篷的体积最大. …………………12分
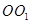 为
为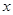 m,则1<x<4.
m,则1<x<4.由题设可得正六棱锥底面边长为(单位:m)
 …………………2分
…………………2分于是底面正六边形的面积为(单位:m2)
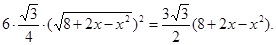 …………………4分
…………………4分帐篷的体积为(单位:m3)
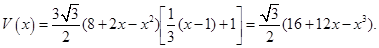 ……………6分
……………6分求导数,得
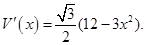 ………………8分
………………8分令
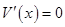 ,解得x=-2(不合题意,舍去),x=2.
,解得x=-2(不合题意,舍去),x=2.当1<x<2时,
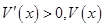 为增函数;当2<x<4时,
为增函数;当2<x<4时,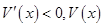 为减函数.
为减函数. 所以当x=2时,
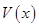 最大. …………………11分
最大. …………………11分答:当
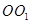 为2m时,帐篷的体积最大. …………………12分
为2m时,帐篷的体积最大. …………………12分略

练习册系列答案
相关题目
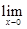
 =-1,则过曲线y=f(x)上点(1,f(1))处的切线斜率为( )
=-1,则过曲线y=f(x)上点(1,f(1))处的切线斜率为( )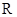 上的函数
上的函数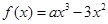 ,其中
,其中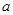 为大于零的常数.
为大于零的常数.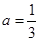 时,令
时,令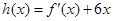 ,求证:当
,求证:当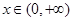 时,
时,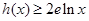 (
(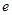 为自然对数的底数);
为自然对数的底数);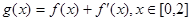 ,在
,在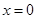 处取得最大值,求
处取得最大值,求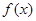 ,当自变量由
,当自变量由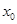 变化到
变化到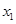 时函数值的增量与相应的自变量的增量比是函数
时函数值的增量与相应的自变量的增量比是函数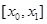 上的平均变化率
上的平均变化率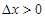
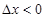
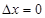
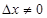
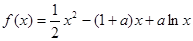 ,其中
,其中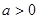 .
.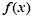 的极小值点;
的极小值点;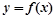 在点
在点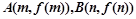 处的切线都与
处的切线都与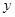 轴垂直,问是否存在常数
轴垂直,问是否存在常数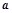 ,使函数
,使函数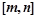 上存在零点?如果存在,求
上存在零点?如果存在,求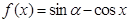 ,则
,则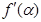 等于( )
等于( )



 ,若
,若 ,则
,则 ( )
( )



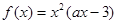 ,其中a为常数.若函数
,其中a为常数.若函数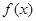 在区间(-1,0)上是增函数,则 a的取值范围是___
在区间(-1,0)上是增函数,则 a的取值范围是___