题目内容
【题目】已知函数![]() (m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是
(m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)设![]() (其中
(其中![]() 为f (x)的导函数),证明:对任意x > 0,都有
为f (x)的导函数),证明:对任意x > 0,都有![]() .
.
(注: ![]() )
)
【答案】(Ⅰ) n = 2,m = 2 (Ⅱ) ![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】试题分析:(1)由切线方程为![]() 得到
得到 ,从中可以解出
,从中可以解出![]() .(2)函数
.(2)函数![]() 的导数
的导数![]() ,观察可以发现当
,观察可以发现当![]() 时,
时, ![]() ,所以
,所以![]() ;当
;当![]() 时,
时, ![]() ,从而得到函数的单调性及其最值.(3)函数
,从而得到函数的单调性及其最值.(3)函数![]() 是一个较为复杂的函数,我们可以把要求证的不等式转化为求证
是一个较为复杂的函数,我们可以把要求证的不等式转化为求证![]() 和
和![]() ,后两个不等式可以通过构建新函数来证明.
,后两个不等式可以通过构建新函数来证明.
解析: (Ⅰ)由![]() ,得
,得![]() ,由已知得
,由已知得![]() ,解得
,解得![]() .又
.又![]() .
.
(Ⅱ)解:由(Ⅰ)得: ![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() ,∴当
,∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,
, ![]() 时,
时, ![]() .
.
(Ⅲ)证: ![]() .对任意
.对任意![]() ,
, ![]() 等价于
等价于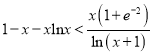 ,令
,令 ![]() ,则
,则 ![]() ,由
,由 ![]() 得:
得: ![]() ,
,
∴当 ![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
所以![]() 的最大值为
的最大值为![]() ,即
,即 ![]() .设
.设![]() ,则
,则 ![]() ,∴当
,∴当![]() 时,
时, ![]() 单调递增,
单调递增, ![]() ,故当
,故当 ![]() 时,
时, ![]() ,即
,即![]() ,
, 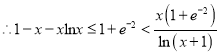 ,∴对任意
,∴对任意![]() ,都有
,都有 ![]() .
.

练习册系列答案
相关题目
【题目】(2016·辽宁五校联考)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个) | 10 | 20 | 30 |
加工时间y(分钟) | 21 | 30 | 39 |
现已求得上表数据的线性回归方程![]() =
=![]() +
+![]() 中的
中的![]() 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A. 84分钟 B. 94分钟
C. 102分钟 D. 112分钟