题目内容
5.在△ABC中,∠A=90°,边AC=1,AB=2,过点A作AP⊥BC交BC于P,且$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λμ=$\frac{4}{25}$.分析 由条件利用两个向量的加减法的法则,以及其几何意义求得$\overrightarrow{AP}$=$\overrightarrow{AC}$+$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AC}$,而已知$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,可得λ和μ的值,从而求得λμ的值.
解答 解:由题意可得BC=$\sqrt{5}$,且△ACP∽△BCA,∴$\frac{CP}{AC}=\frac{AC}{BC}$,即 $\frac{CP}{1}=\frac{1}{\sqrt{5}}$,求得CP=$\frac{\sqrt{5}}{5}$.
∴$\overrightarrow{AP}$=$\overrightarrow{AC}$+$\overrightarrow{CP}$=$\overrightarrow{AC}$+$\frac{1}{5}$$\overrightarrow{CB}$=$\overrightarrow{AC}$+$\frac{1}{5}$($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AC}$,而已知$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ=$\frac{1}{5}$,μ=$\frac{4}{5}$,
∴λμ=$\frac{4}{25}$,
故答案为:$\frac{4}{25}$.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,平面向量基本定理,属于基础题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案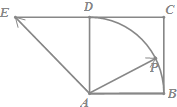 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
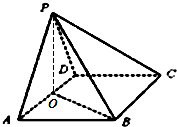 如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.