题目内容
【题目】平面直角坐标系中,在x轴的上方作半径为1的圆Γ,与x轴相切于坐标原点O.平行于x轴的直线l1与y轴交点的纵坐标为-1,A(x,y)是圆Γ外一动点,A与圆Γ上的点的最小距离比A到l1的距离小1.
(Ⅰ)求动点A的轨迹方程;
(Ⅱ)设l2是圆Γ平行于x轴的切线,试探究在y轴上是否存在一定点B,使得以AB为直径的圆截直线l2所得的弦长不变.

【答案】(I)![]() ;(II)存在
;(II)存在![]() 满足题意.
满足题意.
【解析】
(Ⅰ)由题意,圆Γ上距![]() 距离最小的点在
距离最小的点在![]() 上,于是依题意知
上,于是依题意知![]() 的长度等于
的长度等于![]() 到
到![]() 的距离,即可求解;
的距离,即可求解;
(Ⅱ)假设存在这样的点![]() ,设其坐标为
,设其坐标为![]() ,以
,以![]() 为直径的圆的圆心为
为直径的圆的圆心为![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,于是
,于是![]() ,
,![]() ,根据弦长公式建立关系,待定系数法,即可求解
,根据弦长公式建立关系,待定系数法,即可求解![]() 的值,可得其坐标
的值,可得其坐标
解:(Ⅰ)设圆Γ的圆心为O1,显然圆Γ上距A距离最小的点在AO1上,
于是依题意知AO1的长度等于A到l1的距离.显然A不能在l1的下方,
若不然A到l1的距离小于AO1的长度,
故有![]() ,
,
即y=![]() x2(x≠0).
x2(x≠0).
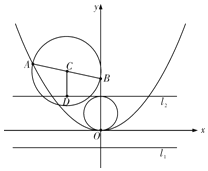
(Ⅱ)若存在这样的点B,设其坐标为(0,t),
以AB为直径的圆的圆心为C,过C作l2的垂线,垂足为D.
则C点坐标为(![]() ),于是CD=
),于是CD=![]() ,
,
AB=![]()
设所截弦长为l,
则![]() =
=![]() CD2=
CD2=![]()
于是l2=(12-4t)y+8t-16,
弦长不变即l不随y的变化而变化,
故12-4t=0,即t=3.
即存在点B(0,3),满足以AB为直径的圆截直线l2所得的弦长不变.

练习册系列答案
相关题目
