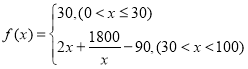题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,作出函数
时,作出函数![]() 的图象;
的图象;
(2)是否存在实数a,使得函数在区间![]() 上有最小值8,若存在求出a的值;若不存在,请说明理由.
上有最小值8,若存在求出a的值;若不存在,请说明理由.

【答案】(1)图象见解析;(2)存在![]() 或
或![]() 满足条件,理由见解析.
满足条件,理由见解析.
【解析】
(1)将![]() 代入,去绝对值,然后做出函数图象即可;
代入,去绝对值,然后做出函数图象即可;
(2)分![]() ,
,![]() 和
和![]() 三种情况,结合二次函数的性质讨论函数在
三种情况,结合二次函数的性质讨论函数在![]() 上的最小值,令其等于8,可求出答案.
上的最小值,令其等于8,可求出答案.
(1)当![]() 时,
时,![]() ,
,
图象见下图:
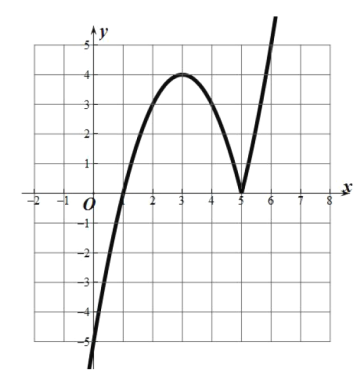
(2)假设存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有最小值8,
上有最小值8,
![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,
,
函数![]() 的对称轴为
的对称轴为![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,解得
,解得![]() ,符合题意;
,符合题意;
②当![]() 时,
时,![]() 不可能有最小值8(舍去);
不可能有最小值8(舍去);
③当![]() 时,
时,![]() ,
,
![]() 是开口向下的二次函数,对称轴为
是开口向下的二次函数,对称轴为![]() ,
,
只需比较![]() 和
和![]() 的大小,
的大小,
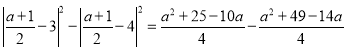
![]() ,
,
若![]() ,
,![]()
![]() ,此时
,此时![]() 在
在![]() 时取得最小值,即
时取得最小值,即![]() ,解得
,解得![]() ,不符合题意,舍去;
,不符合题意,舍去;
若![]() ,
,![]()
![]() ,此时
,此时![]() 在
在![]() 时取得最小值,即
时取得最小值,即![]() ,解得
,解得![]() ,符合题意.
,符合题意.
综上,![]() 或
或![]() .
.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】已知△ABC的边AB所在直线方程为y=3x,BC所在直线方程为y=ax+12,AC边上的高BD所在直线方程为y=﹣x+8.
(1)求实数a的值;
(2)若AC边上的高BD![]() ,求边AC所在的直线方程.
,求边AC所在的直线方程.
【题目】2018年4月4日召开的国务院常务会议明确将进一步推动网络提速降费工作落实,推动我国数字经济发展和信息消费,今年移动流量资费将再降![]() 以上,为响应国家政策,某通讯商计划推出两款优惠流量套餐,详情如下:
以上,为响应国家政策,某通讯商计划推出两款优惠流量套餐,详情如下:
套餐名称 | 月套餐费/元 | 月套餐流量/M |
A | 30 | 3000 |
B | 50 | 6000 |
这两款套餐均有以下附加条款:套餐费用月初一次性收取,手机使用流量一旦超出套餐流量,系统就会自动帮用户充值![]() 流量,资费20元;如果又超出充值流量,系统再次自动帮用户充值
流量,资费20元;如果又超出充值流量,系统再次自动帮用户充值![]() 流量,资费20元,以此类推.此外,若当月流量有剩余,系统将自动清零,不可次月使用.
流量,资费20元,以此类推.此外,若当月流量有剩余,系统将自动清零,不可次月使用.
小张过去50个月的手机月使用流量(单位:M)的频数分布表如下:
月使用流量分组 |
|
|
|
|
|
|
频数 | 4 | 5 | 11 | 16 | 12 | 2 |
根据小张过去50个月的手机月使用流量情况,回答以下几个问题:
(1)若小张选择A套餐,将以上频率作为概率,求小张在某一个月流量费用超过50元的概率;
(2)小张拟从A或B套餐中选定一款,若以月平均费用作为决策依据,他应订哪一种套餐?说明理由.