题目内容
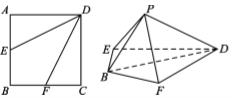
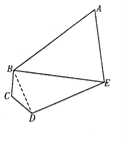
【题目】如图，某旅游区拟建一主题游乐园，该游乐区为五边形区域ABCDE，其中三角形区域ABE为主题游乐区，四边形区域为BCDE为休闲游乐区，AB、BC，CD，DE，EA，BE为游乐园的主要道路（不考虑宽度）．
.
（I）求道路BE的长度；
（Ⅱ）求道路AB，AE长度之和的最大值．
【答案】（Ⅰ）
;（Ⅱ） 
.
【解析】
试题分析：（Ⅰ）连结
,
内，可根据余弦定理求,从而可以判断和
的形状，在内根据勾股定理求
;（Ⅱ）设
,
,
,在
内，根据正弦定理，表示
,
,利用三角函数的有界性，得到长度和的最大值.
试题解析：（Ⅰ）如图，连接,在中，由余弦定理得：
,
,
,
,
又
,
,
所以在
中，
;
（Ⅱ）设,,,
在中，由正弦定理，得
,
,
，
，
，
，
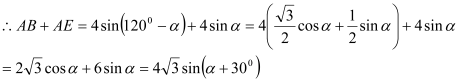
当
，即
时，取得最大值，
即道路
长度之和的最大值为.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
