题目内容
【题目】在直二面角α﹣l﹣β中,A∈α,B∈β,A,B都不在l上,AB与α所成角为x,AB与β所成角为y,AB与l所成角为z,则cos2x+cos2y+sin2z的值为( )
A.![]() B.2C.3D.
B.2C.3D.![]()
【答案】B
【解析】
根据题意,先分别作出AB与α所成角为x,AB与β所成角为y,AB与l所成角为z,再利用三角函数求解即可.
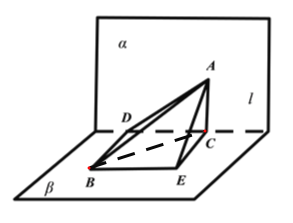
过A、B分别作AC⊥l于C,BD⊥l于D,过B作直线平行于l,过C作直线平行于BD,两直线交于E,连接AD、AC、AE.
因α一l一β为直二面角,BD在β上,l=α∩β,BD⊥l,故BD⊥α.同理AC⊥β.
又∠BAD、∠ABC分别为AB与α、β所成的角,有∠BAD=x,∠ABC=y.
又EC∥BD,EC⊥l,AC⊥β,有AE⊥l,AE⊥BE,∠EBA=z.
∴cos2x+cos2y+sin2z=![]()
![]()
![]()
![]() .
.
故选:B.

练习册系列答案
相关题目