题目内容
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
【答案】(1)见解析(2)见解析
【解析】
(1)结合正弦定理,条件选择①![]() ,则
,则![]() ,再利用公式
,再利用公式![]() 求
求![]() ;
;
若选择条件②,由正弦定理和诱导公式可得![]() ,再根据二倍角公式求得
,再根据二倍角公式求得![]() ,再根据
,再根据![]() 求解.
求解.
(2)解法1:设![]() ,在
,在![]() 中由余弦定理,解得
中由余弦定理,解得![]() ,再由(1)
,再由(1)![]() ,解得
,解得![]() 边长,最后求得到
边长,最后求得到![]() 的面积;解法2:由
的面积;解法2:由![]() 可知,
可知,![]() ,,再根据正弦定理和面积公式
,,再根据正弦定理和面积公式![]()
![]() .
.
解:若选择条件①,则答案为:
(1)在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() .
.
(2)解法1:设![]() ,易知
,易知![]()
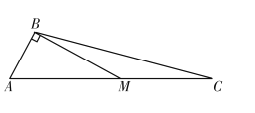
在![]() 中由余弦定理得:
中由余弦定理得:![]() ,解得
,解得![]() .
.
所以![]()
在![]() 中,
中,
![]()
所以![]() ,所以
,所以![]() ,
,
所以![]()
解法2:因为![]() ,所以
,所以![]() ,
,
因为![]() 所以
所以![]() ,
,
所以![]()
因为![]() 为锐角,所以
为锐角,所以![]()
又![]()
所以![]()
![]()
所以![]()
![]()
若选择条件②,则答案为:
(1)因为![]() ,所以
,所以![]() ,
,
由正弦定理得![]() ,
,
因为![]() ,所以
,所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
则![]() ,所以
,所以![]() .
.
(2)同选择①

练习册系列答案
相关题目