题目内容
【题目】如图，在三棱柱
中，
，
，平面
平面
，
与
相交于点
.
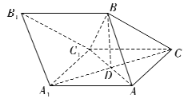
（1）求证：
；
（2）求二面角
的正弦值．
【答案】（1）详见解析（2）
【解析】
（1）由四边形
为菱形可得
，由面面垂直性质可得
平面
，由线面垂直性质可证得结论；（2）由三棱柱特点可得
，由三线合一性质可得
，根据线面垂直判定定理可证得
平面，从而可以
为原点建立空间直角坐标系，利用二面角的向量求法求得法向量夹角的余弦值，进而得到法向量夹角的正弦值，即为所求二面角的正弦值.
（1）
四边形为菱形 
平面
平面，平面
平面
，
平面
平面，又
平面 
（2）
由三棱柱的特点可知：
为
中点 
平面，平面 
平面，
平面
以为原点，可建立如下图所示的空间直角坐标系
，
，
，
则
，
平面 平面的一个法向量为：
设平面
的法向量
，令
，则
，
即二面角
的正弦值为：
练习册系列答案
阅读快车系列答案
相关题目
【题目】某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种，
方案一：每满200元减50元；
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、l个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
（1）若两个顾客都选择方案二，各抽奖一次，求至少一个人获得半价优惠的概率；
（2）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
