题目内容
(本小题满分10分)
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
(1) a=2 (2) (-∞,5).
解析试题分析:解法一:(1)由f(x)≤3,得|x-a|≤3,解得a-3≤x≤a+3.
又已知不等式f(x)≤3的解集为{x|-1≤x≤5},
所以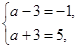 解得a=2.
解得a=2.
(2)当a=2时,f(x)=|x-2|.设g(x)=f(x)+f(x+5),
于是g(x)=|x-2|+|x+3|=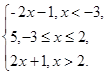
所以当x<-3时,g(x)>5;当-3≤x≤2时,g(x)=5;当x>2时,g(x)>5.
综上可得,g(x)的最小值为5.
从而,若f(x)+f(x+5)≥m,即g(x)≥m对一切实数x恒成立,
则m的取值范围为(-∞,5].
解法二:(1)同解法一.
(2)当a=2时,f(x)=|x-2|,设g(x)=f(x)+f(x+5).
由|x-2|+|x+3|≥|(x-2)-(x+3)|=5(当且仅当-3≤x≤2时等号成立)得,g(x)的最小值为5.
从而,若f(x)+f(x+5)≥m,即g(x)≥m对一切实数x恒成立,
则m的取值范围为(-∞,5).
考点:绝对值不等式的解法;函数恒成立问题.
点评:本题考查函数恒成立问题,绝对值不等式的解法,考查转化思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
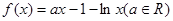
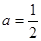 时,求函数在
时,求函数在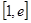 上的最大值和最小值;
上的最大值和最小值;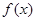 在
在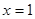 处取得极值,不等式
处取得极值,不等式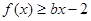 对
对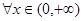 恒成立,求实数
恒成立,求实数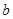 的取值范围。
的取值范围。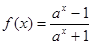 (a>1).
(a>1).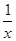 在(0,1)上是减函数.
在(0,1)上是减函数.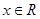 .
.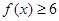 的解集;
的解集;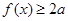 对
对

 时的值域;
时的值域; 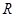 的函数
的函数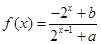 是奇函数。
是奇函数。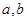 的值;
的值;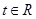 ,不等式
,不等式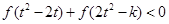 恒成立,求
恒成立,求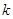 的取值范围;
的取值范围; 。
。 。
。 ,讨论
,讨论 的单调性;
的单调性; 恒有
恒有 ,求
,求 的取值范围。
的取值范围。