题目内容
已知函数 。
。
(Ⅰ)设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅱ)若对任意 恒有
恒有 ,求
,求 的取值范围。
的取值范围。
(I) 所以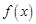 在各区间内的增减性如下表:
在各区间内的增减性如下表:
(II)a的取值范围为(区间 ( 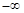 ,
, )
)(  ,t)
,t)(t,1) (1,+ 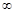 )
)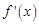 的符号
的符号+ 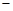
+ + 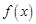 的单调性
的单调性增函数 减函数 增函数 增函数 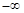 ,2)
,2)
解析试题分析:(I) 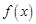 的定义域为(
的定义域为(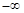 ,1)
,1)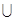 (1,
(1,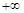 )
)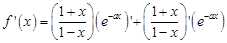

因为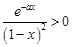 (其中
(其中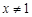 )恒成立,所以
)恒成立,所以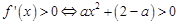
⑴ 当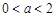 时,
时,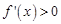 在(
在(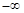 ,0)
,0)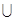 (1,
(1,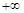 )上恒成立,所以
)上恒成立,所以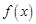 在(
在(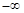 ,1)
,1)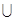 (1,
(1,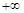 )上为增函数;
)上为增函数;
⑵ 当 时,
时,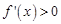 在(
在(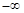 ,0)
,0)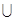 (0,1)
(0,1)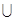 (1,
(1,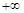 )上恒成立,所以
)上恒成立,所以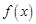 在(
在(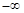 ,1)
,1)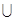 (1,
(1,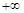 )上为增函数;
)上为增函数;
⑶ 当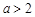 时,
时,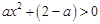 的解为:(
的解为:(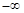 ,
, )
)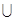 (t,1)
(t,1)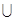 (1,+
(1,+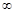 )
)
(其中 )
)
所以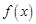 在各区间内的增减性如下表:
在各区间内的增减性如下表:区间 ( 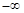 ,
, )
)(  ,t)
,t)(t,1) (1,+ 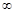 )
)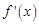 的符号
的符号+ 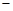
+ + 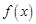 的单调性
的单调性增函数 减函数 增函数 增函数
(II)显然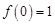

练习册系列答案
相关题目
 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 在区间
在区间 上是减函数.
上是减函数. 的值;
的值; 在
在 上恒成立,求实数
上恒成立,求实数 的最大值;
的最大值; 的方程
的方程 有且只有一个实数根,求
有且只有一个实数根,求 的值.
的值. 。
。 的单调区间;
的单调区间; 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;

 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围; ,若
,若 的图象与
的图象与 上有两个交点,求
上有两个交点,求 的取值范围。
的取值范围。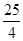 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
 上是单调函数
上是单调函数  。
。 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围。
的取值范围。 。
。 在
在 上的单调性;
上的单调性; 在
在 上有极值,求
上有极值,求 的取值范围。
的取值范围。