题目内容
设函数f(x)="|x-1|" +|x-a|,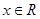 .
.
(I)当a =4时,求不等式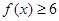 的解集;
的解集;
(II)若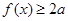 对
对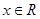 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(I) 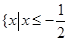 或
或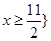 (II)
(II) 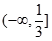
解析试题分析:(Ⅰ)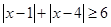 等价于
等价于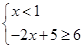 或
或 或
或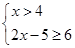 ,
,
解得: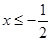 或
或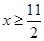 .
.
故不等式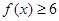 的解集为
的解集为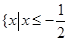 或
或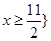 . ……5分
. ……5分
(Ⅱ)因为: 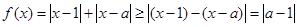 (当
(当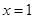 时等号成立)
时等号成立)
所以: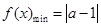 ……8分
……8分
由题意得: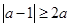 ,解得
,解得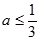 ,∴
,∴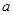 的取值范围
的取值范围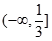 . ……10分
. ……10分
考点:本小题主要考查含绝对值的不等式的解法和恒成立问题.
点评:对于含绝对值的不等式,要想办法把绝对值号去掉,可以利用绝对值的几何意义,也可以分类讨论;求解恒成立问题,一般转化为最值问题解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,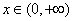 ,是否存在实数
,是否存在实数 ,使
,使 同时满足下列两个条件:(1)
同时满足下列两个条件:(1) 上是减函数,在
上是减函数,在 上是增函数;(2)
上是增函数;(2) ,若存在,求出
,若存在,求出 (
( ≠0)在区间(-1,1)上的单调性。
≠0)在区间(-1,1)上的单调性。 ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.  的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明 ,使得
,使得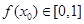 ,且
,且 ,求证:
,求证: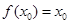

 的最小正周期;
的最小正周期; 对任意
对任意 ,有
,有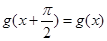 ,且当
,且当 时,
时, ;求函数
;求函数 上的解析式。
上的解析式。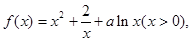
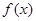 在
在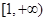 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 对于区间
对于区间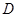 上的任意两个值
上的任意两个值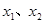 总有以下不等式
总有以下不等式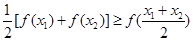 成立,则称函数
成立,则称函数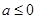 时,
时, ,
, .其中
.其中 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 .
. 的奇偶性,并说明理由;
的奇偶性,并说明理由;
 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围; ,若
,若 的图象与
的图象与 上有两个交点,求
上有两个交点,求 的取值范围。
的取值范围。