题目内容
【题目】某公司研发了两种具有自主知识产权的操作系统，分别命名为“天下”、“东方”.这两套操作系统均适用于手机、电脑、车联网、物联网等，且较国际同类操作系统更加流畅.
（1）为了解喜欢“天下”系统是否与性别有关，随机调查了
名男用户和名女用户，每位用户对“天下”系统给出喜欢或不喜欢的评价，得到下面列联表：
请问：能否有
的把握认为男、女用户对“天下”系统的喜欢有差异？
附：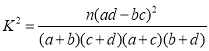
.
（2）该公司选定
万名用户对“天下”和“东方”操作系统（以下简称“天下”、“东方”）进行测试，每个用户只能从“天下”或“东方”中选择一个使用，每经过一个月后就给用户一次重新选择“天下”或“东方”的机会.这个月选择“天下”的用户在下个月选择“天下”的概率均为
，选择“东方”的概率均为
，
；这个月选择“东方”的用户在下个月选择“天下”的概率均为
，选择“东方”的概率均为
，
.记
表示第
个月用户选择“天下”的概率，已知
，
，
，
，
.
（ⅰ）求
的值；
（ⅱ）证明：数列
（）为等比数列；
（ⅲ）预测选择“天下”操作系统的用户数量不超过多少万人.（精确到1万）
【答案】（1）有95%的把握认为“男、女用户对天下”系统的喜欢有差异；（2）（ⅰ）
，（ⅱ）见解析，（ⅲ）不超过
万人
【解析】
（1）将2×2列联表中的数据代入到K2的公式中即可得解；（2）（ⅰ）利用题干给出的Pn+1和Pn的等量关系，列出关于α和β的方程组，即可解得α和β的值；（ⅱ）在（ⅰ）的基础上，用定义法来判定等比数列；（ⅲ）求出用户选择“天下”操作系统的概率，即可求出用户数量．
（1）由表可知，a＝10，b＝20，c＝40，d＝30，
所以
，
故能有95%的把握认为男、女用户对“天下”系统的喜欢有差异．
（2）（ⅰ）由题知：
，且
，
，
，
所以
，得
所以
解得：
（ⅱ）由（ⅰ）知：
所以
又因为
，所以
所以
（
）为首项等于
，公比等于
的等比数列.
（ⅲ）由（ⅱ）知：
所以
（当
越大时，
越接近
）
所以依据概率预测选择“天下”操作系统的用户数量不超过万人.
