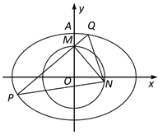
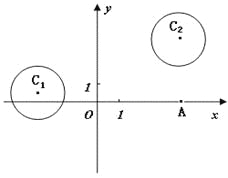
题目内容
【题目】如图为一块边长为2km的等边三角形地块ABC，为响应国家号召，现对这块地进行绿化改造，计划从BC的中点D出发引出两条成60°角的线段DE和DF，与AB和AC围成四边形区域AEDF，在该区域内种上草坪，其余区域修建成停车场，设∠BDE＝
．
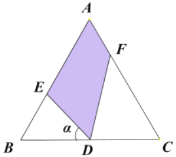
（1）当＝60°时，求绿化面积；
（2）试求地块的绿化面积
的取值范围．
【答案】（1）
（2）
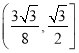
【解析】
（1）当
时，DE∥AC，DF∥AB，四边形
是平行四边形，
和
均为边长为
的等边三角形，再求绿化面积；（2）先求出
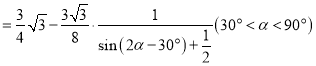，再求地块的绿化面积
的取值范围．
(1)当时，DE∥AC，DF∥AB，四边形是平行四边形，和均为边长为的等边三角形，面积都是
，
所以绿化面积为
.
（2）由题意知，
，在中，
，
由正弦定理是
，所以
，
在
中，
，
，
由正弦定理得
，所以
，
所以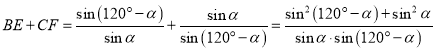
.
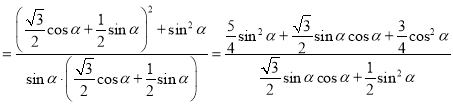
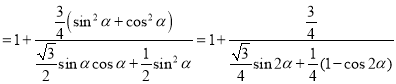
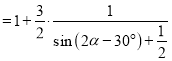所以
，
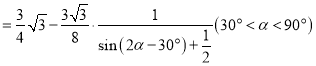当，
，
，所以
.
答:地块的绿化面积
的取值范围是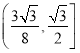
.
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水x(单位：千克)清洗该蔬菜1千克后，蔬菜上残留的农药y(单位：微克)的数据作了初步处理，得到下面的散点图及一些统计量的值．
y（微克）
x（千克）
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | －121 | －751 |
其中
（I）根据散点图判断，
与
，哪一个适宜作为蔬菜农药残量
与用水量
的回归方程类型（给出判断即可，不必说明理由）；
(Ⅱ)若用解析式与用水量的回归方程，求出与的回归方程．(c，d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药，当它的残留量低于20微克时对人体无害，为了放心食用该蔬菜，请估计需要用多少千克的清水清洗一千克蔬菜？(精确到0.1，参考数据
)
附：参考公式：回归方程
中斜率和截距的最小二乘估计公式分别为：
【题目】随着经济的发展，个人收入的提高，自2019年1月1日起，个人所得税起征点和税率的调整.调整如下：纳税人的工资、薪金所得，以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表，调整前后的计算方法如下表：
个人所得税税率表（调整前） | 个人所得税税率表（调整后） | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率（ | 级数 | 全月应纳税所得额 | 税率（ |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
（1）假如小红某月的工资、薪金等所得税前收入总和不高于8000元，记
表示总收入，
表示应纳的税，试写出调整前后关于的函数表达式；
（2）某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入，并制成下面的频数分布表：
收入 （元） |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在
及
的人群中按分层抽样抽取7人，再从中选2人作为新纳税法知识宣讲员，求两个宣讲员不全是同一收入人群的概率；
（3）小红该月的工资、薪金等税前收入为7500元时，请你帮小红算一下调整后小红的实际收入比调整前增加了多少？
