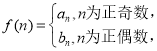题目内容
【题目】已知函数![]() 是奇函数(其中
是奇函数(其中![]() )
)
(1)求实数m的值;
(2)已知关于x的方程![]() 在区间
在区间![]() 上有实数解,求实数k的取值范围;
上有实数解,求实数k的取值范围;
(3)当![]() 时,
时,![]() 的值域是
的值域是![]() ,求实数n与a的值.
,求实数n与a的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)由f(x)是奇函数,f(﹣x)=﹣f(x),结合对数的真数大于0求出m的值;
(2)由题意问题转化为求函数![]() 在x∈[2,6]上的值域,求导判断出单调性,进而求得值域,可得k的范围.
在x∈[2,6]上的值域,求导判断出单调性,进而求得值域,可得k的范围.
(3)先判定函数的单调性,进而由x![]() 时,f(x)的值域为(1,+∞),根据函数的单调性得出n与a的方程,从而求出n、a的值.
时,f(x)的值域为(1,+∞),根据函数的单调性得出n与a的方程,从而求出n、a的值.
(1)∵f(x)是奇函数,
∴f(﹣x)=﹣f(x),
∴loga![]() loga
loga![]() loga
loga![]() ,
,
∴![]() ,
,
即1﹣m2x2=1﹣x2对一切x∈D都成立,
∴m2=1,m=±1,
由于![]() 0,∴m=﹣1;
0,∴m=﹣1;
(2)由(1)得,![]() ,∴
,∴![]()
即![]() ,令
,令![]() ,
,
则![]() ,
,
∴![]() 在区间
在区间![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;所以,
;所以,![]() .
.
(3)由(1)得,![]() ,且
,且![]()
∵![]() 在
在![]() 与
与![]() 上单调递减
上单调递减
∵x∈(n,a﹣2![]() ),定义域D=(﹣∞,﹣1)∪(1,+∞),
),定义域D=(﹣∞,﹣1)∪(1,+∞),
①当n≥1时,则1≤n<a﹣2![]() ,即a>1+2
,即a>1+2![]() ,
,
∴f(x)在(n,a﹣2![]() )上为减函数,值域为(1,+∞),
)上为减函数,值域为(1,+∞),
∴f(a﹣2![]() )=1,
)=1,
即![]() a,
a,
∴a![]() 3,或a
3,或a![]() 1(不合题意,舍去),且n=1;
1(不合题意,舍去),且n=1;
②当n<1时,则(n,a﹣2![]() )(﹣∞,﹣1),
)(﹣∞,﹣1),
∴n<a﹣2![]() 1,
1,
即a<2![]() 1,
1,
且f(x)在(n,a﹣2![]() )上的值域是(1,+∞);
)上的值域是(1,+∞);
∴f(a﹣2![]() )=1,
)=1,
即![]() a,
a,
解得a![]() 3(不合题意,舍去),或a
3(不合题意,舍去),或a![]() 1;
1;
此时n=﹣1(舍去);
综上,a![]() 3,n=1.
3,n=1.

【题目】某租车公司给出的财务报表如下:
年度 项目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接单量(单) | 14463272 | 40125125 | 60331996 |
油费(元) | 214301962 | 581305364 | 653214963 |
平均每单油费 | 14.82 | 14.49 | |
平均每单里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为![]() .
.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里).