题目内容
设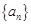 为等差数列,从
为等差数列,从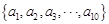 中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
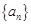 为等差数列,从
为等差数列,从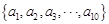 中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。24
解:设等差数列{an}的公差为d,
当取出4个数的公差为d时,有下列情况:
a1,a2,a3,a4;a2,a3,a4,a5;…;a7,a8,a9,a10,共7组;
当取出4个数的公差为2d时,有下列情况:
a1,a3,a5,a7;a2,a4,a6,a8;a3,a5,a7,a9;a4,a6,a8,a10,共4组;
当取出4个数的公差为3d时,有下列情况:
a1,a4,a7,a10,共1组,
综上,共有12种情况;
同理,当取出4个数的公差分别为-d,-2d,-3d时,共有12种情况,
则这样的等差数列最多有24个
当取出4个数的公差为d时,有下列情况:
a1,a2,a3,a4;a2,a3,a4,a5;…;a7,a8,a9,a10,共7组;
当取出4个数的公差为2d时,有下列情况:
a1,a3,a5,a7;a2,a4,a6,a8;a3,a5,a7,a9;a4,a6,a8,a10,共4组;
当取出4个数的公差为3d时,有下列情况:
a1,a4,a7,a10,共1组,
综上,共有12种情况;
同理,当取出4个数的公差分别为-d,-2d,-3d时,共有12种情况,
则这样的等差数列最多有24个

练习册系列答案
相关题目
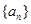 满足
满足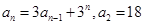
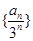 为等差数列;(2)求
为等差数列;(2)求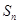 。
。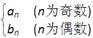 ,求数列{cn}的前101项之和T101;
,求数列{cn}的前101项之和T101; 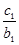 +
+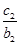 +…+
+…+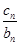 =an+1成立,求c1+c2+…+c2012的值.
=an+1成立,求c1+c2+…+c2012的值.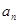 }是等差数列,且
}是等差数列,且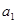 =12,
=12,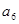 =27,
=27,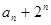 }的前
}的前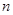 项和
项和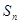
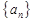 的前
的前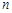 项和为
项和为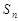 ,
,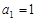 ,且
,且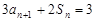 (
(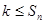 恒成立,求实数
恒成立,求实数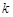 的最大值
的最大值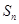 为等差数列
为等差数列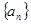 的前n项和,且
的前n项和,且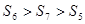 ,有下列四个命题:
,有下列四个命题: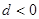 ;(2)
;(2)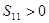 ;(3)
;(3)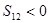 ;(4)数列
;(4)数列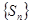 中的最大项为
中的最大项为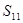 .其中正确命题的序号是________.
.其中正确命题的序号是________.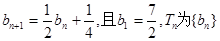 的前n项和。
的前n项和。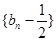 是等比数列,并求
是等比数列,并求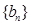 的通项公式;
的通项公式;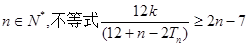 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。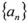 为等差数列,
为等差数列,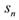 为其前n项和,且
为其前n项和,且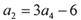 ,则
,则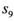 =
=