题目内容
已知数列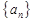 的前
的前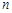 项和为
项和为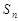 ,
,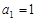 ,且
,且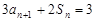 (
(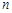 为正整数)
为正整数)
(Ⅰ)求出数列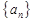 的通项公式;
的通项公式;
(Ⅱ)若对任意正整数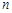 ,
,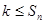 恒成立,求实数
恒成立,求实数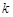 的最大值
的最大值
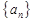 的前
的前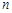 项和为
项和为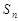 ,
,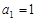 ,且
,且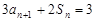 (
(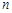 为正整数)
为正整数)(Ⅰ)求出数列
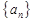 的通项公式;
的通项公式;(Ⅱ)若对任意正整数
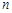 ,
,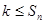 恒成立,求实数
恒成立,求实数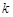 的最大值
的最大值(1) (
(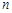 为正整数).
为正整数).
(2)实数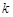 的最大值为1.
的最大值为1.
 (
(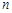 为正整数).
为正整数).(2)实数
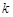 的最大值为1.
的最大值为1.(I)再构造一个当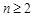 时,
时, 然后与
然后与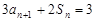 作差,可得到
作差,可得到 ,从而可知是
,从而可知是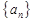 等比数列,问题得解.
等比数列,问题得解.
(II)此题的关键是求Sn的最小值,要先根据前n项和公式求出Sn,然后从函数的角度研究其单调性确定其最值即可.
(1)
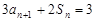 , ①
, ①  当
当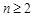 时,
时, . ②
. ②
由 ① - ②,得 .
. 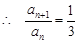
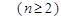 .
.
又 ,
, ,解得
,解得  .
.
 数列
数列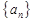 是首项为1,公比为
是首项为1,公比为 的等比数列.
的等比数列.
 (
(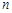 为正整数). ……………………6分
为正整数). ……………………6分
(2)由(Ⅰ)知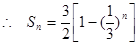
由题意可知,对于任意的正整数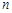 ,恒有
,恒有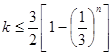 ,
,
 数列
数列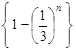 单调递增, 当
单调递增, 当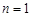 时,该数列中的最小项为
时,该数列中的最小项为 ,
,
 必有
必有 ,即实数
,即实数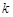 的最大值为1.
的最大值为1.
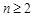 时,
时, 然后与
然后与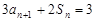 作差,可得到
作差,可得到 ,从而可知是
,从而可知是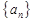 等比数列,问题得解.
等比数列,问题得解.(II)此题的关键是求Sn的最小值,要先根据前n项和公式求出Sn,然后从函数的角度研究其单调性确定其最值即可.
(1)

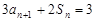 , ①
, ①  当
当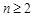 时,
时, . ②
. ② 由 ① - ②,得
 .
. 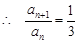
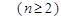 .
. 又
 ,
, ,解得
,解得  .
.  数列
数列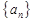 是首项为1,公比为
是首项为1,公比为 的等比数列.
的等比数列. (
(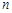 为正整数). ……………………6分
为正整数). ……………………6分(2)由(Ⅰ)知
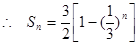
由题意可知,对于任意的正整数
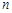 ,恒有
,恒有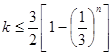 ,
, 数列
数列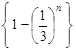 单调递增, 当
单调递增, 当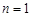 时,该数列中的最小项为
时,该数列中的最小项为 ,
,  必有
必有 ,即实数
,即实数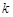 的最大值为1.
的最大值为1. 
练习册系列答案
相关题目
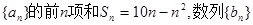 的每一项都有
的每一项都有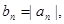 求数列
求数列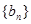 的前n项和
的前n项和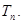
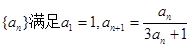
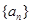 的通项公式;
的通项公式;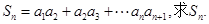
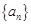 为等差数列,从
为等差数列,从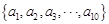 中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。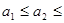 …
…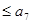 ,其中
,其中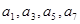 成公比为
成公比为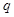 的等比数列,
的等比数列,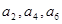 成公差为1的等差数列,则
成公差为1的等差数列,则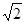
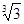
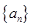 中,
中,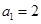 ,
,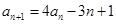 ,
,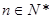 .
.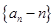 是等比数列;
是等比数列;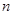 项和
项和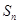 ;
;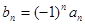 ,求数列
,求数列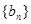 的前
的前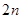 项和
项和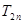 。
。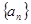 中,有
中,有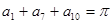 ,则
,则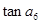 = ▲ 。
= ▲ 。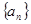 为等差数列,
为等差数列,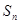 是其前n项的和,且
是其前n项的和,且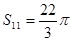 ,则
,则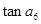 =( )
=( )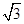
 是等差数列
是等差数列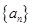 的前
的前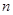 项和,且
项和,且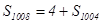 ,则
,则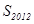 的值为( )
的值为( )