题目内容
已知等差数列{an}的首项a1=1,公差d>0,且其第二项、第五项、第十四项分别是等比数列{bn}的第二、三、四项.
(1)求数列{an}与{bn}的通项公式;
(2)令数列{cn}满足:cn=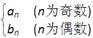 ,求数列{cn}的前101项之和T101;
,求数列{cn}的前101项之和T101;
(3)设数列{cn}对任意n∈N*,均有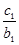 +
+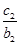 +…+
+…+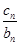 =an+1成立,求c1+c2+…+c2012的值.
=an+1成立,求c1+c2+…+c2012的值.
(1)求数列{an}与{bn}的通项公式;
(2)令数列{cn}满足:cn=
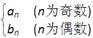 ,求数列{cn}的前101项之和T101;
,求数列{cn}的前101项之和T101; (3)设数列{cn}对任意n∈N*,均有
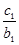 +
+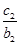 +…+
+…+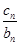 =an+1成立,求c1+c2+…+c2012的值.
=an+1成立,求c1+c2+…+c2012的值.(1)an=2n-1. bn=3n-1
(2)5151+
(3)c1+c2+…+c2012=3+2×3+2×32+…+2×32011=32012.
(2)5151+

(3)c1+c2+…+c2012=3+2×3+2×32+…+2×32011=32012.
(1) 第二项、第五项、第十四项分别是等比数列{bn}的第二、三、四项,可建立关于d,b1,q的三个方程解方程组即可求解.
(2) 解本题关键是T101=(a1+a3+…+a101)+(b2+b4+…+b100).然后分组求和即可.
(3)先根据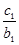 +
+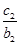 +…+
+…+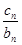 =an+1,求出{
=an+1,求出{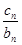 }的通项公式,然后根据通项公式的特点采用数列求和的方法求和即可.
}的通项公式,然后根据通项公式的特点采用数列求和的方法求和即可.
(1)由题意得:(a1+d)(a1+13d)=(a1+4d)2 (d>0),
解得d=2,∴an=2n-1. …………………………………………2分
∴b2=a2=3, b3=a5=9,∴bn=3n-1 …………………………………………4分
(2)∵a101=201,b2=3
∴T101=(a1+a3+…+a101)+(b2+b4+…+b100)=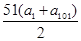 +
+
=5151+ …………………10分
…………………10分
(3)当n≥2时,由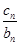 =
=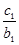 +
+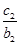 +…+
+…+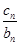 -(
-(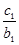 +
+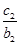 +…+
+…+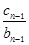 )=an+1-an=2
)=an+1-an=2
得cn=2bn=2·3n-1,
当n=1时,c1=3.故cn= ……………………………13分
……………………………13分
故c1+c2+…+c2012=3+2×3+2×32+…+2×32011=32012.
(2) 解本题关键是T101=(a1+a3+…+a101)+(b2+b4+…+b100).然后分组求和即可.
(3)先根据
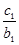 +
+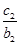 +…+
+…+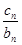 =an+1,求出{
=an+1,求出{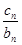 }的通项公式,然后根据通项公式的特点采用数列求和的方法求和即可.
}的通项公式,然后根据通项公式的特点采用数列求和的方法求和即可.(1)由题意得:(a1+d)(a1+13d)=(a1+4d)2 (d>0),
解得d=2,∴an=2n-1. …………………………………………2分
∴b2=a2=3, b3=a5=9,∴bn=3n-1 …………………………………………4分
(2)∵a101=201,b2=3
∴T101=(a1+a3+…+a101)+(b2+b4+…+b100)=
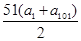 +
+
=5151+
 …………………10分
…………………10分(3)当n≥2时,由
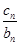 =
=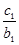 +
+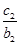 +…+
+…+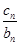 -(
-(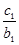 +
+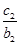 +…+
+…+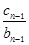 )=an+1-an=2
)=an+1-an=2得cn=2bn=2·3n-1,
当n=1时,c1=3.故cn=
 ……………………………13分
……………………………13分故c1+c2+…+c2012=3+2×3+2×32+…+2×32011=32012.

练习册系列答案
相关题目
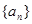 满足
满足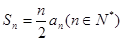 ,
,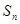 是
是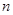 项的和,并且
项的和,并且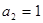 .
.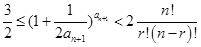
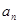 )满足
)满足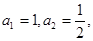 并且
并且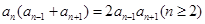 ,则数列的第2012项为
,则数列的第2012项为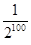
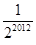
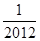
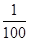
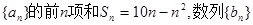 的每一项都有
的每一项都有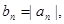 求数列
求数列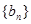 的前n项和
的前n项和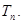
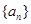 的公差
的公差 ,若
,若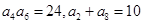 ,则该数列的前
,则该数列的前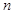 项和
项和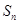 的最大值为( )
的最大值为( )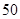
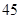
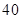
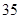
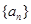 是一个等差数列,且
是一个等差数列,且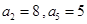 .等比数列
.等比数列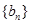 的前
的前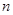 项和为
项和为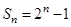 .
.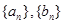 的通项公式;
的通项公式;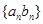 的最大项及相应
的最大项及相应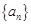 为等差数列,从
为等差数列,从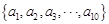 中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。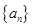 中,若
中,若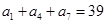 ,,
,, 则前9项和等于( )
则前9项和等于( )  中,
中, 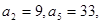 则
则