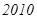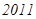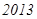题目内容
数列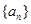 满足
满足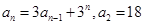
(1)证明数列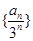 为等差数列;(2)求
为等差数列;(2)求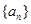 的前n项和
的前n项和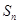 。
。
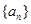 满足
满足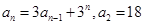
(1)证明数列
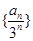 为等差数列;(2)求
为等差数列;(2)求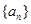 的前n项和
的前n项和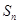 。
。(1)证明见解析 (2)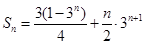
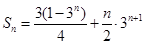
(1)由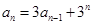 两边除以
两边除以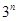 后再根据等差数列的定义直接可以证明。
后再根据等差数列的定义直接可以证明。
(2)在(1)的基础上先求出{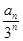 }的通项公式,进而确定
}的通项公式,进而确定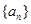 的通项公式,再根据数列求和的方法求和即可。
的通项公式,再根据数列求和的方法求和即可。
解: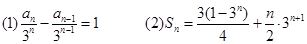
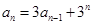 两边除以
两边除以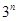 后再根据等差数列的定义直接可以证明。
后再根据等差数列的定义直接可以证明。(2)在(1)的基础上先求出{
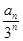 }的通项公式,进而确定
}的通项公式,进而确定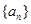 的通项公式,再根据数列求和的方法求和即可。
的通项公式,再根据数列求和的方法求和即可。解:
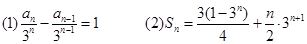

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
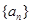 的通项公式;
的通项公式;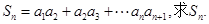
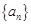 为等差数列,从
为等差数列,从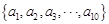 中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。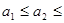 …
…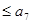 ,其中
,其中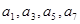 成公比为
成公比为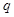 的等比数列,
的等比数列,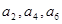 成公差为1的等差数列,则
成公差为1的等差数列,则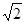
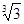
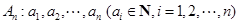 ,定义“
,定义“ 变换”:
变换”: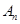 变换成数列
变换成数列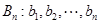 ,其中
,其中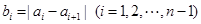 ,且
,且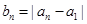 ,这种“
,这种“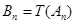 .继续对数列
.继续对数列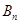 进行“
进行“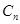 ,…,依此类推,当得到的数列各项均为
,…,依此类推,当得到的数列各项均为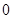 时变换结束.
时变换结束.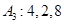 和
和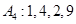 经过不断的“
经过不断的“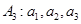 经过有限次“
经过有限次“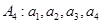 一定能经过有限次“
一定能经过有限次“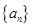 为等差数列,
为等差数列,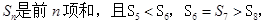 则下列结论错误的是( )
则下列结论错误的是( ) 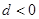
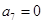
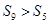
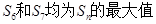
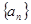 中,
中, 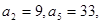 则
则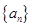 的前n项和为
的前n项和为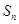 ,若
,若 则
则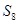 = ;
= ;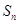 是等差数列
是等差数列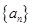 的前
的前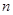 项和,且
项和,且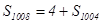 ,则
,则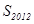 的值为( )
的值为( )