题目内容
(本小题满分12分)已知圆 经过
经过 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上.
(1)求圆 的方程;
的方程;
(2)若直线 经过点
经过点 且与圆
且与圆 相切,求直线
相切,求直线 的方程.
的方程.
 经过
经过 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上. (1)求圆
 的方程;
的方程; (2)若直线
 经过点
经过点 且与圆
且与圆 相切,求直线
相切,求直线 的方程.
的方程.(1)

(2)
 或
或 .
.解(1)设圆 的方程为
的方程为
 ,
,
 依题意得:
依题意得:
解得 .
.
所以圆 的方程为
的方程为 .
.
圆心为 的圆的半径长
的圆的半径长 .
.
所以圆 的方程为
的方程为 . ……6分
. ……6分
(2)由于直线 经过点
经过点 ,
,
当直线 的斜率不存在时,
的斜率不存在时, 与圆
与圆
 相离.
相离.
当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为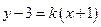 ,
,
即: .
.
因为直线 与圆
与圆 相切,且圆
相切,且圆 的圆心为
的圆心为 ,半径为
,半径为 ,所以有
,所以有
 .
.
解得 或
或 .
. 
所以直线 的方程为
的方程为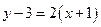 或
或 ,
,
即: 或
或 . ……12分
. ……12分
 的方程为
的方程为
 ,
,  依题意得:
依题意得:
解得
 .
. 所以圆
 的方程为
的方程为 .
. 圆心为
 的圆的半径长
的圆的半径长 .
. 所以圆
 的方程为
的方程为 . ……6分
. ……6分 (2)由于直线
 经过点
经过点 ,
,当直线
 的斜率不存在时,
的斜率不存在时, 与圆
与圆
 相离.
相离. 当直线
 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为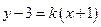 ,
, 即:
 .
. 因为直线
 与圆
与圆 相切,且圆
相切,且圆 的圆心为
的圆心为 ,半径为
,半径为 ,所以有
,所以有 .
. 解得
 或
或 .
. 
所以直线
 的方程为
的方程为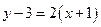 或
或 ,
,即:
 或
或 . ……12分
. ……12分
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
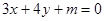 与圆
与圆 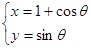 (
(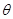 为参数)至少有一个公共点,则实数m的取值范围是
为参数)至少有一个公共点,则实数m的取值范围是  和圆
和圆 相交于点A、B,则弦AB的垂直平分线方程是. .
相交于点A、B,则弦AB的垂直平分线方程是. .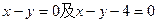 都相切,圆心在直线
都相切,圆心在直线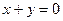 上,则圆C的方程为
上,则圆C的方程为


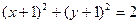
 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。 ,求圆C的方程;
,求圆C的方程; 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。 和圆
和圆 相交于点A、B,则弦AB的垂直平分线方程是 .
相交于点A、B,则弦AB的垂直平分线方程是 .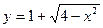 (
(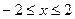 )与直线
)与直线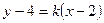 有两个交点时,实数
有两个交点时,实数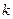 的取值范围是
的取值范围是  截直线
截直线 所得的弦长等于 。
所得的弦长等于 。