题目内容
【题目】在平面直角坐标系
中，点
，若在曲线
上存在点
使得
，则实数
的取值范围为__________
【答案】
【解析】
根据题意，设P（x，y），分析可得若|PB|＝2|PA|，则有（x﹣4）2+y2＝4（x﹣1）2+4y2，变形可得x2+y2＝4，进而可得P的轨迹为以O为圆心，半径为2的圆；将曲线C的方程变形为（x﹣a）2+（y﹣2a）2＝9，可得以（a，2a）为圆心，半径为3的圆；据此分析可得若曲线C上存在点P使得|PB|＝2|PA|，则圆C与圆x2+y2＝4有公共点，由圆与圆的位置关系可得3﹣2
2+3，解可得a的取值范围，即可得答案．
根据题意，设P（x，y），
若|PB|＝2|PA|，即|PB|2＝4|PA|2，则有（x﹣4）2+y2＝4（x﹣1）2+4y2，
变形可得：x2+y2＝4，
即P的轨迹为以O为圆心，半径为2的圆，
曲线Cx2﹣2ax+y2﹣4ay+5a2﹣9＝0，即（x﹣a）2+（y﹣2a）2＝9，则曲线C是以（a，2a）为圆心，半径为3的圆；
若曲线C上存在点P使得|PB|＝2|PA|，则圆C与圆x2+y2＝4有公共点，
则有3﹣22+3，即1
|a|≤5，
解可得：
a
或
a，
即a的取值范围为：[
，
]∪[
，
]；
故答案为：[，]∪[，]．
【题目】在对人们的休闲方式的一次调查中，用简单随机抽样方法调查了125人，其中女性70人，男性55人.女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外35人主要的休闲方式是运动.
（1）根据以上数据建立一个
列联表；
（2）能否在犯错误的概率不超过0.025的前提下，认为性别与休闲方式有关系?
（3）在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座，讲座结束后再从这6人中抽取2人作反馈交流，求参加交流的恰好为2位女性的概率.
附：
P（ | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
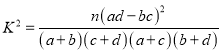
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |
【题目】在某区“创文明城区”（简称“创城”）活动中，教委对本区
四所高中学校按各校人数分层抽样，随机抽查了100人，将调查情况进行整理后制成下表：
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
（注：参与率是指：一所学校“创城”活动中参与的人数与被抽查人数的比值）假设每名高中学生是否参与”创城”活动是相互独立的.
（1）若该区共2000名高中学生，估计
学校参与“创城”活动的人数；
（2）在随机抽查的100名高中学生中，随机抽取1名学生，求恰好该生没有参与“创城”活动的概率；
（3）在上表中从
两校没有参与“创城”活动的同学中随机抽取2人，求恰好两校各有1人没有参与“创城”活动的概率是多少？
