题目内容
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)![]() 的定义域为
的定义域为![]() ,求导可得
,求导可得![]() .则考查函数的单调性只需考查二次函数
.则考查函数的单调性只需考查二次函数![]() 的性质可得:
的性质可得:
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减.
上单调递减.
(2)原问题等价于![]() ,
, ![]() 恒成立. 构造函数,令
恒成立. 构造函数,令![]() ,则
,则![]() ,
, ![]() ,即
,即![]() 在
在![]() 时取得最大值.
时取得最大值.
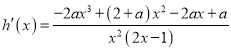 .由
.由![]() 解得
解得![]() .经检验可得a=1符合题意.故
.经检验可得a=1符合题意.故![]() .
.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, ![]() .
.
∵![]() .
.
令![]() ,则
,则
(a)若![]() ,即当
,即当![]() 时,对任意
时,对任意![]() ,
, ![]() 恒成立, 即当
恒成立, 即当![]() 时,
时, ![]() 恒成立(仅在孤立点处等号成立).
恒成立(仅在孤立点处等号成立).
∴![]() 在
在![]() 上单调递增.
上单调递增.
(b)若![]() ,即当
,即当![]() 或
或![]() 时,
时, ![]() 的对称轴为
的对称轴为![]() .
.
①当![]() 时,
时, ![]() ,且
,且![]() .
.
如图,任意![]() ,
, ![]() 恒成立, 即任意
恒成立, 即任意![]() 时,
时, ![]() 恒成立,
恒成立,
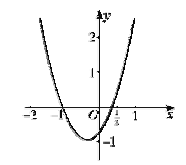
∴![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,
时, ![]() ,且
,且![]() .
.
如图,记![]() 的两根为
的两根为![]()
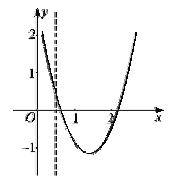
∴当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
∴当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减.
上单调递减.
(2)![]() 恒成立等价于
恒成立等价于![]() ,
, ![]() 恒成立.
恒成立.
令![]() ,则
,则![]() 恒成立等价于
恒成立等价于![]() ,
, ![]()
![]() .
.
要满足![]() 式,即
式,即![]() 在
在![]() 时取得最大值.
时取得最大值.
∵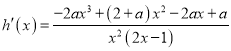 .
.
由![]() 解得
解得![]() .
.
当![]() 时,
时, 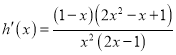 ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,从而
上单调递减,从而![]() ,符合题意.
,符合题意.
所以, ![]() .
.

练习册系列答案
相关题目