题目内容
【题目】设数列{an}为等差数列，且a5=14，a7=20，数列{bn}的前n项和为Sn ， b1= 
且3Sn=Sn﹣1+2（n≥2，n∈N）．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）若cn=anbn ， n=1，2，3，…，Tn为数列{cn}的前n项和，Tn＜m对n∈N*恒成立，求m的最小值．
【答案】解：（Ⅰ） 数列{an}为等差数列，公差d= 
（a7﹣a5）=3，易得a1=2，
所以an=3n﹣1
由3Sn=Sn﹣1+2（n≥2，n∈N），得3Sn=Sn﹣bn+2，即bn=2﹣2Sn ，
所以b2=2﹣（b1+b2）
， 又 
，所以b2= 
， 
= 
由3Sn=Sn﹣1+2，当n≥3时，得3Sn﹣1=Sn﹣2+2，
两式相减得：3（Sn﹣Sn﹣1）=Sn﹣1﹣Sn﹣2 ， 即3bn=bn﹣1 ， 所以 
= （n≥3）
又 = ，所以{bn}是以 为首项， 为公比的等比数列，于是bn=2 
（Ⅱ）cn=anbn=2（3n﹣1） ，
∴Tn=2[2 +5 
+8 
+…+（3n﹣1） ]， Tn=2[2 +5 +…+（3n﹣4） +（3n﹣1） 
]，
两式相减得 Tn=2[3 +3 +3 +…+3 ﹣ ﹣（3n﹣1） ]
=2[1+ + + +…+ 
﹣ ﹣（3n﹣1） ]
=2×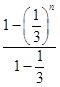 
﹣ 
﹣2（3n﹣1）
所以Tn= 
﹣ ﹣ 
，
从而Tn= ﹣ ﹣ ＜ ，
∵Tn＜m对n∈N+恒成立，∴m≥ ∴m的最小值是 
【解析】（Ⅰ）依题意，可求得等差数列{an}的公差d=3，a1=2，从而可得数列{an}的通项公式；再由b1= 
且3Sn=Sn﹣1+2（n≥2，n∈N），可求得 
= 
（n≥3）， 
= ，从而可得{bn}是以 
为首项， 为公比的等比数列，于是可求{bn}的通项公式；（Ⅱ）cn=anbn=2（3n﹣1） 
，利用错位相减法可求得{cn}的前n项和Tn ， 依题意可得Tn＜m对n∈N*恒成立时m的最小值．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系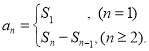
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
