题目内容
【题目】已知函数![]() ,直线
,直线![]() 与
与![]() 的图象的相邻两个交点的横坐标分别是
的图象的相邻两个交点的横坐标分别是![]() 和
和![]() ,现有如下命题:
,现有如下命题:
①该函数在![]() 上的值域是
上的值域是![]() ;
;
②在![]() 上,当且仅当
上,当且仅当![]() 时函数取最大值;
时函数取最大值;
③该函数的最小正周期可以是![]() ;
;
④![]() 的图象可能过原点.
的图象可能过原点.
其中的真命题有__________.(写出所有真命题的序号)
【答案】④
【解析】当![]() 时,区间
时,区间![]() 没有意义,故①错误;该函数在
没有意义,故①错误;该函数在![]() 上,当
上,当![]() 时函数取最小值,故②错误;由周期公式
时函数取最小值,故②错误;由周期公式![]() ,得
,得![]() ,此时
,此时![]() ,由
,由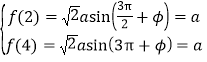 ,计算得出
,计算得出![]() ,不满足
,不满足![]() ,可以知道该函数的最小正周期不可以是
,可以知道该函数的最小正周期不可以是![]() ,故③错误;由
,故③错误;由![]() ,得
,得![]() ,即
,即![]() 时
时![]() 的图象过原点,故④正确.∴正确命题的序号是④,故答案为④.
的图象过原点,故④正确.∴正确命题的序号是④,故答案为④.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查三角函数函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,对存在性问题可以用特值法进行排除,还要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目